CONCEPTION D'UN CAPTEUR CAPACITIF
Conception et fabrication d'un digicode à distance variable
1 - Introduction
Depuis son invention dans les années 1960, le digicode a révolutionné la manière dont nous sécurisons nos espaces et nos biens. Initialement conçu pour remplacer les clés physiques par des codes d'accès, ce système a rapidement gagné en popularité grâce à sa simplicité et son efficacité. Toutefois, avec l'évolution des technologies, le digicode traditionnel montre aujourd'hui certaines limites, telles que la vulnérabilité aux vols de codes notamment en utilisant les marques d'usures laissés sur les touches ou la potentielle transmission de maladies à travers l'usage des touches physiques. C'est dans ce contexte que notre système de digicode à détection de proximité et à plusieurs positions vient répondre à certaines de ces problématiques. Notre dispositif d'authentification offre une alternative à la fois plus sécurisée avec des combinaisons plus complexes, intuitive et sans contact direct avec le dispositif. Grâce à l'utilisation de plusieurs électrodes et à la détection de la distance du doigt de l'utilisateur, notre digicode permet de créer des combinaisons d'avantage complexes rendant ainsi le vol de codes plus difficile.
1.1 - Problématique et objectifs
L'évolution des technologies et des besoins en matière de sécurité a mis en évidence certaines limitations des digicodes traditionnels. Ces dispositifs, bien que largement adoptés, présentent des vulnérabilités telles que le vol de codes d'accès, qui peut se produire par l'observation des marques d'usure laissées sur les touches. De plus, la manipulation répétée des touches par plusieurs utilisateurs pose des problèmes d'hygiène, favorisant la transmission de bactéries. Face à ces défis, le projet vise à concevoir un digicode à détection de proximité et à plusieurs positions.
Les objectifs spécifiques du projet sont les suivants :
- Sécurité améliorée : L'utilisation de combinaisons plus complexes, rendues possibles par la détection de la distance entre le doigt et le capteur, rend le vol de codes d'accès plus difficile. Cette approche ajoute une couche de sécurité par rapport aux digicodes traditionnels.
- Hygiène : En éliminant le besoin de contact physique avec le dispositif, notre digicode réduit les risques de transmission de maladies. Ce système sans contact est particulièrement pertinent dans des contextes où l'hygiène est une préoccupation majeure.
- Intuitivité et ergonomie : La création d'une interface utilisateur intuitive, qui permet une utilisation sans contact, vise à rendre le dispositif plus facile et agréable à utiliser. Les utilisateurs peuvent ainsi interagir avec le digicode de manière naturelle et sans effort.
1.2 - Méthodes et solutions techniques retenues
Pour atteindre les objectifs fixés, plusieurs méthodes et solutions techniques ont été mises en place :
- Capteurs capacitifs : Le projet utilise des capteurs capacitifs pour détecter la proximité et la position du doigt de l'utilisateur. Chaque capteur est capable de distinguer entre deux positions : proche ou éloigné du capteur.
- Circuit conditionneur : Un circuit conditionneur a été conçu pour traiter et générer le signal des électrodes. Ce circuit inclut un circuit de charge à courant constant, qui fournit un courant stable au condensateur formé par l'électrode et la main de l'utilisateur. Il comporte également un oscillateur avec un comparateur à hystérésis, qui détecte le seuil de déclenchement et permet le fonctionnement en boucle fermée. Ce conditionneur est essentiel pour assurer une détection précise et fiable des positions du doigt.
- Microcontrôleur STM32 : Le projet intègre un microcontrôleur STM32 pour l'acquisition et le traitement du signal. Ce microcontrôleur convertit les variations de capacité en données numériques et gère les différentes combinaisons possibles des positions détectées par les capteurs. Il constitue le cœur du système, assurant la coordination des différentes fonctions du digicode.
- Conception du PCB sous KiCAD : Le schéma et le routage du circuit imprimé (PCB) ont été réalisés à l'aide du logiciel KiCAD. Cette étape permet d'intégrer de manière optimale les différents composants électroniques sur le PCB, facilitant ainsi la fabrication et les tests du dispositif. KiCAD offre une plateforme robuste pour la conception et la simulation des circuits électroniques.
- Programmation et test : Le développement du logiciel embarqué a été une étape cruciale pour assurer le bon fonctionnement du système de digicode à plusieurs positions. Des tests rigoureux ont été effectués pour mesurer les performances et valider la robustesse du dispositif.
2 - Présentation générale du projet
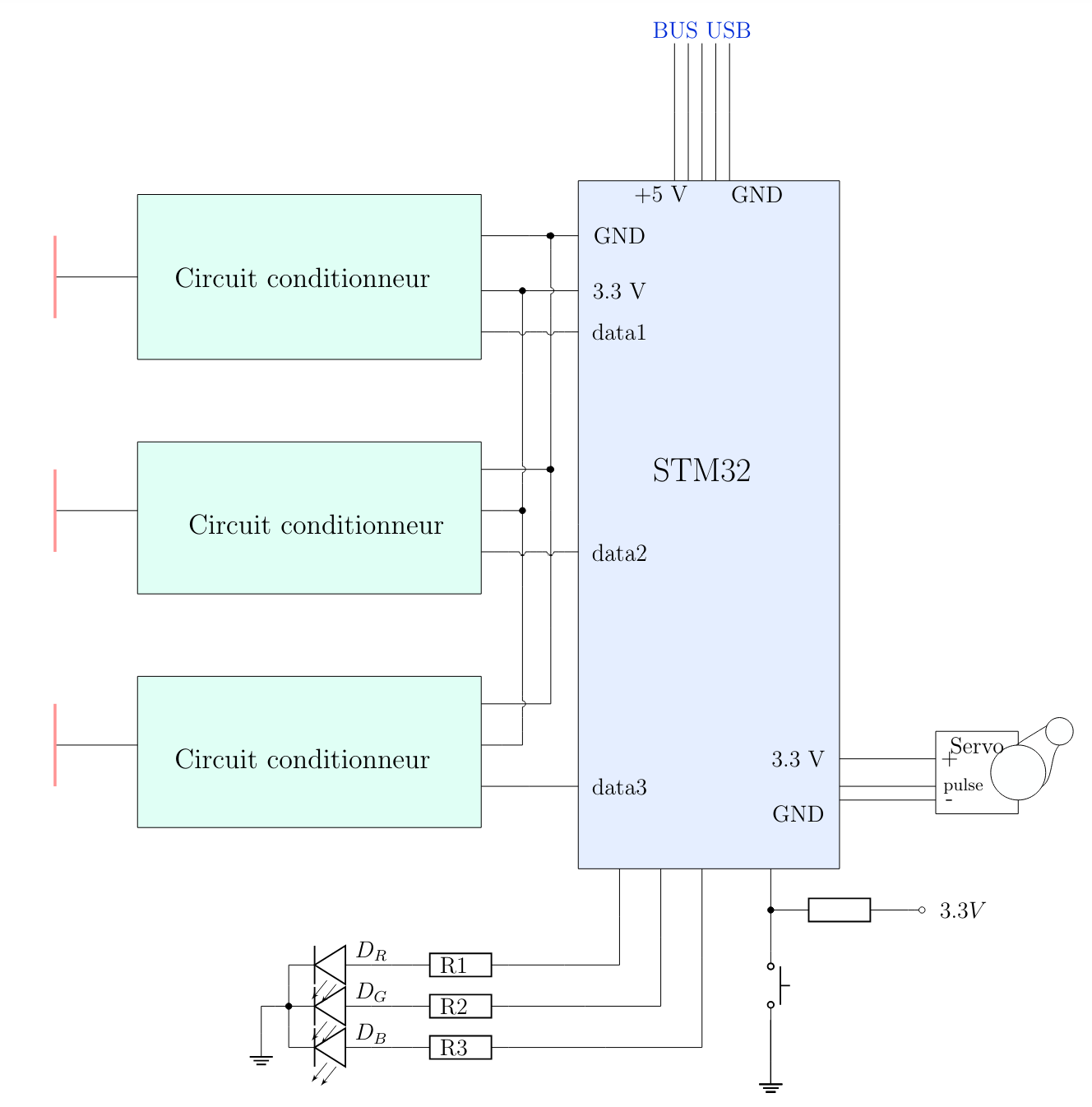
2.1 - Les capteurs capacitifs
Les capteurs capacitifs sont représentent les élements centraux du projet. Leur principe de fonctionnement repose sur la mesure de la capacité électrique entre une électrode et la main de l'utilisateur. Cette capacité varie en fonction de la distance qui les sépare, permettant ainsi de détecter la proximité et la position du doigt sans contact physique.
L'objectif est de créer un condensateur à capacité variable. Dans le modèle théorique du condensateur plan infini, la capacité \(C\) est exprimée comme suit : \[ C = \frac{\varepsilon_0 \varepsilon_r S}{d} \]
où : \(\varepsilon_0\) est la permittivité du vide, \(\varepsilon_r\) est la permittivité relative du matériau entre les plaques, \(S\) est la surface des plaques et \(d\) est la distance entre les plaques.
La démonstration de la formule est à la section 7.2 - Démonstrations
Bien que nos condensateurs ne soient pas infinis, l'approximation est bien assez précise pour l'application visée.
Dans notre application, bien que le modèle du condensateur plan infini ne soit pas strictement valide, il illustre la relation inversement proportionnelle entre la capacité et la distance \(d\) entre l'électrode et la main de l'utilisateur. La capacité est également directement proportionnelle à la surface de l'électrode.
En pratique, nous utilisons trois électrodes pour générer les différentes combinaisons du digicode. Une simulation sous Comsol montre la distribution des lignes de champ électrique lorsqu'une main est placée au-dessus de l'électrode centrale. Les lignes de champ des électrodes adjacentes se courbent vers la main, influençant la mesure de la capacité de l'électrode centrale.
2.2 - Nécessité d’un Conditionneur
Pour exploiter les variations de capacité mesurées par les capteurs capacitifs, un conditionneur de signal est nécessaire. Ce circuit doit traiter et générer le signal des électrodes de manière fiable.
En effet, il est compliqué de mesurer directement la capacité. On pourrait par exemple utiliser la résonnance d'un circuit RLC ou un pont de Sauty-Wien. Cependant ces méthodes sont en général moins précises, plus compliquées à étalonner et également plus sensible au bruit ambiant. La méthode de charge d'un condensateur à courant constant permet le meilleur compromis pour obtenir la meilleure précision.
2.3 - Fonctionnement du Conditionneur
La méthode de détermination de la capacité consiste à charger le condensateur à courant constant. La capacité est alors déduite du temps nécessaire pour atteindre un certain seuil de tension. Cette approche nécessite un circuit précis et stable pour garantir des mesures fiables.
La conception du conditionneur comprend plusieurs composants clés :
- Circuit de charge à courant constant : Ce circuit charge le condensateur formé par la main de l'utilisateur et l'électrode avec un courant constant, permettant de déterminer la capacité en fonction du temps de charge.
- Oscillateur avec comparateur à hystérésis : Utilisé pour détecter le seuil de déclenchement et permettre un fonctionnement en boucle fermée.
2.4 - Système de digicode à plusieurs positions
Initialement, chaque électrode est calibrée pour mesurer une capacité de base en l'absence de tout objet conducteur à proximité. Ensuite, un seuil de détection est défini pour déterminer 2 différentes zones de proximité de la main par rapport à chaque capteur : Proche et éloignée.
Lorsqu'une main s'approche des électrodes, le microcontrôleur détecte les variations de capacité et évalue la distance de la main. Une combinaison de touches et de distances peut être enregistrée comme code d'accès. Par exemple, une séquence de touches pourrait être :
"Capteur 2 proche + Capteur 1 éloigné puis proche + Capteur 3 éloigné". Le système valide ensuite le code en comparant la combinaison entrée par l'utilisateur avec celle préalablement enregistrée. Si les distances et les séquences des capteurs correspondent, l'accès est accordé.
3 - Conception du capteur capacitif
Nous allons dans un premier temps étudier le principal général de fonctionnement du capteur capacitif. Nous étudierons ensuite pourquoi il est nécessaire d'avoir un conditionneur pour traiter et générer le signal de l'électrode. Nous détaillerons par la suite la conception d'un tel conditionneur et enfin nous mènerons des tests et mesures du circuit conditionneur.
3.1 - Principe de fonctionnement
L'objectif est de construire un condensateur à capacité variable. Dans le modèle du condensateur plan infini (sans effets de bord) la capacité s'exprime comme : \(C = \frac{\varepsilon_{0}\varepsilon_{r}S}{d}\). Bien que le modèle du condensateur plan infini n'est pas valide ici, il permet de donner la variation de la capacité en fonction de l'épaisseur d entre les deux armatures (ici l'électrode et la main de l'utilisateur) : La capacité est alors inversement proportionnelle à la distance inter-armature. D'autre part, la capacité est directement proportionnelle à la surface de l'électrode.
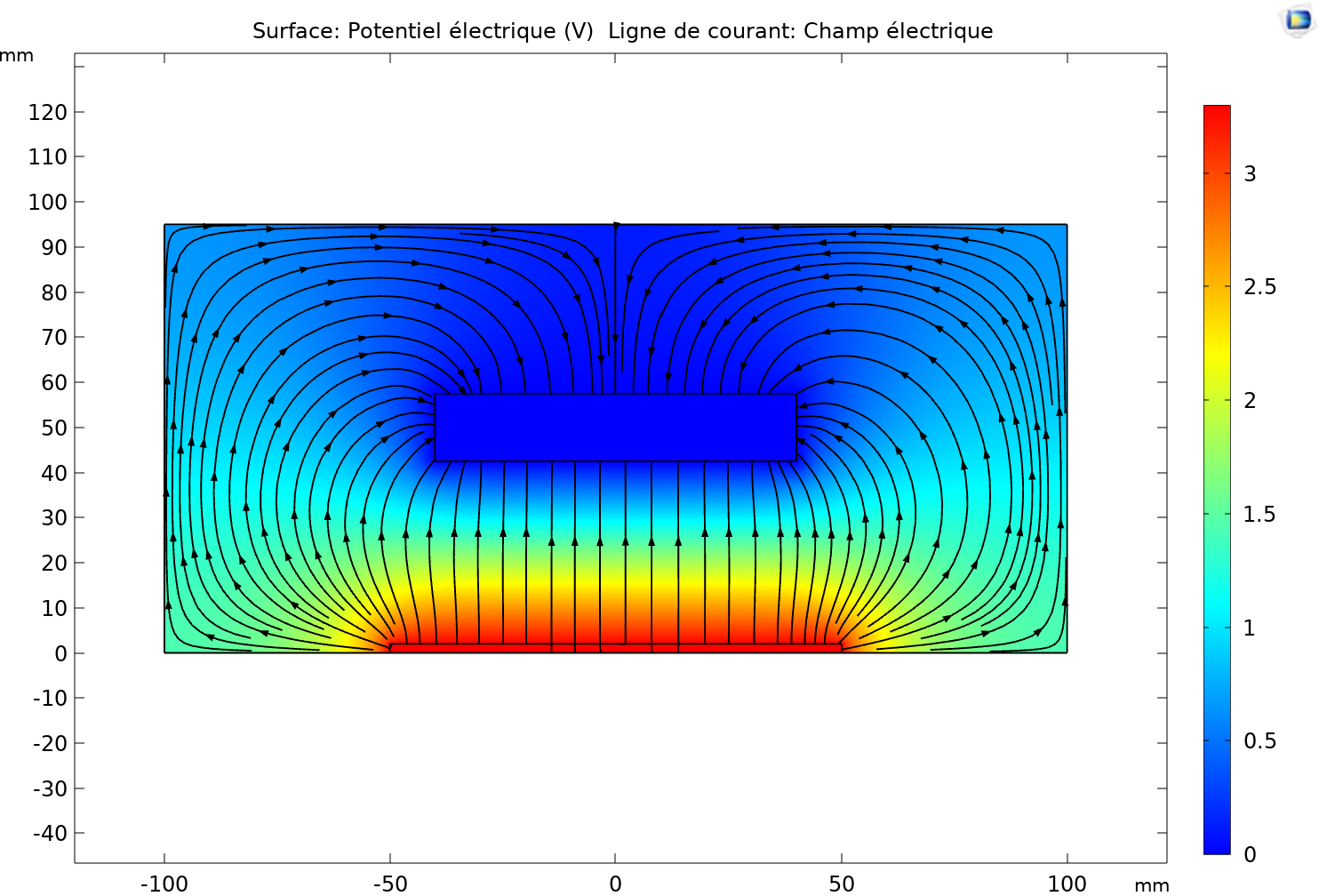
En pratique on utilisera 3 électrode pour les combinaisons du digicode. Après simulation, en plaçant la main au dessus de l'électrode centrale on obtient la simulation suivante :
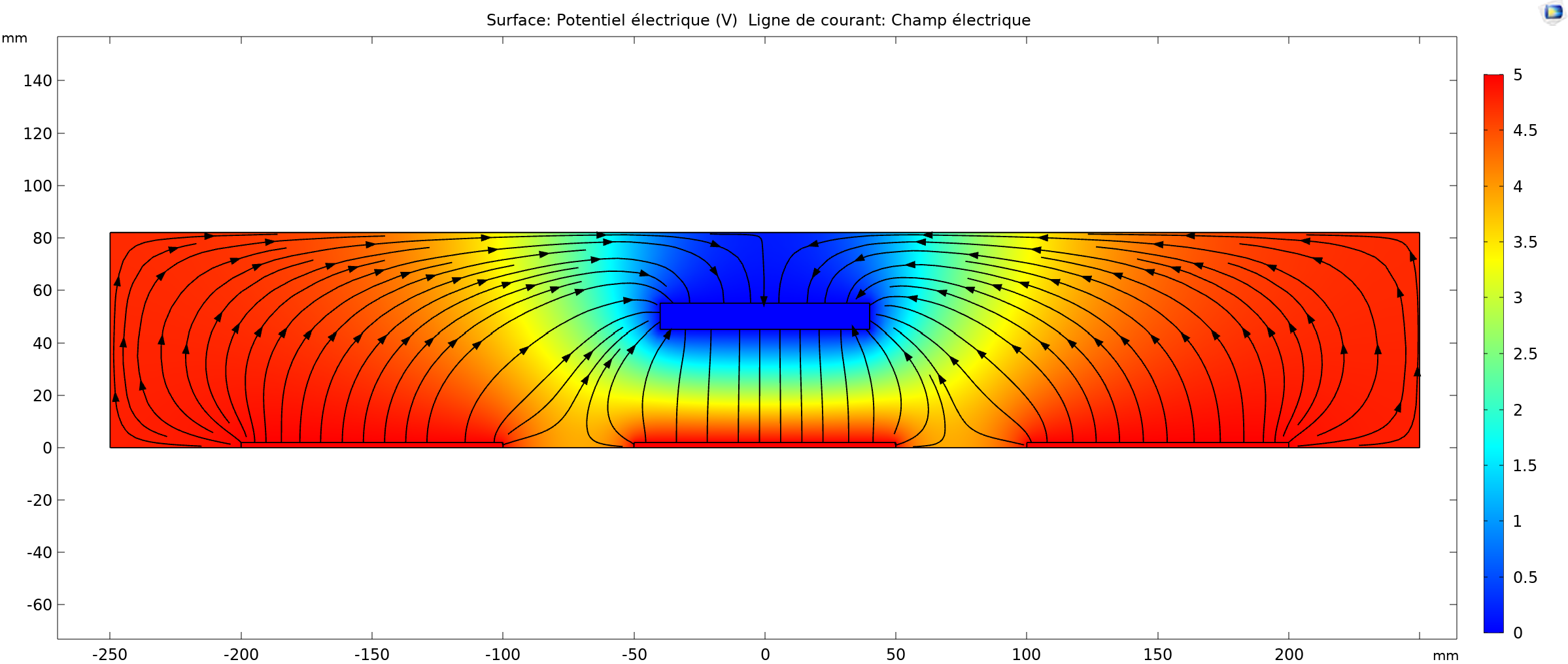
Entre les deux simulations, on constate que les lignes de champs des électrodes placées de part et d'autre de l'électrode dont on souhaite mesurer la capacité, se recourbe sur la main.
On souhaite donc estimer l'erreur engendrée par la présence des autres électrodes.
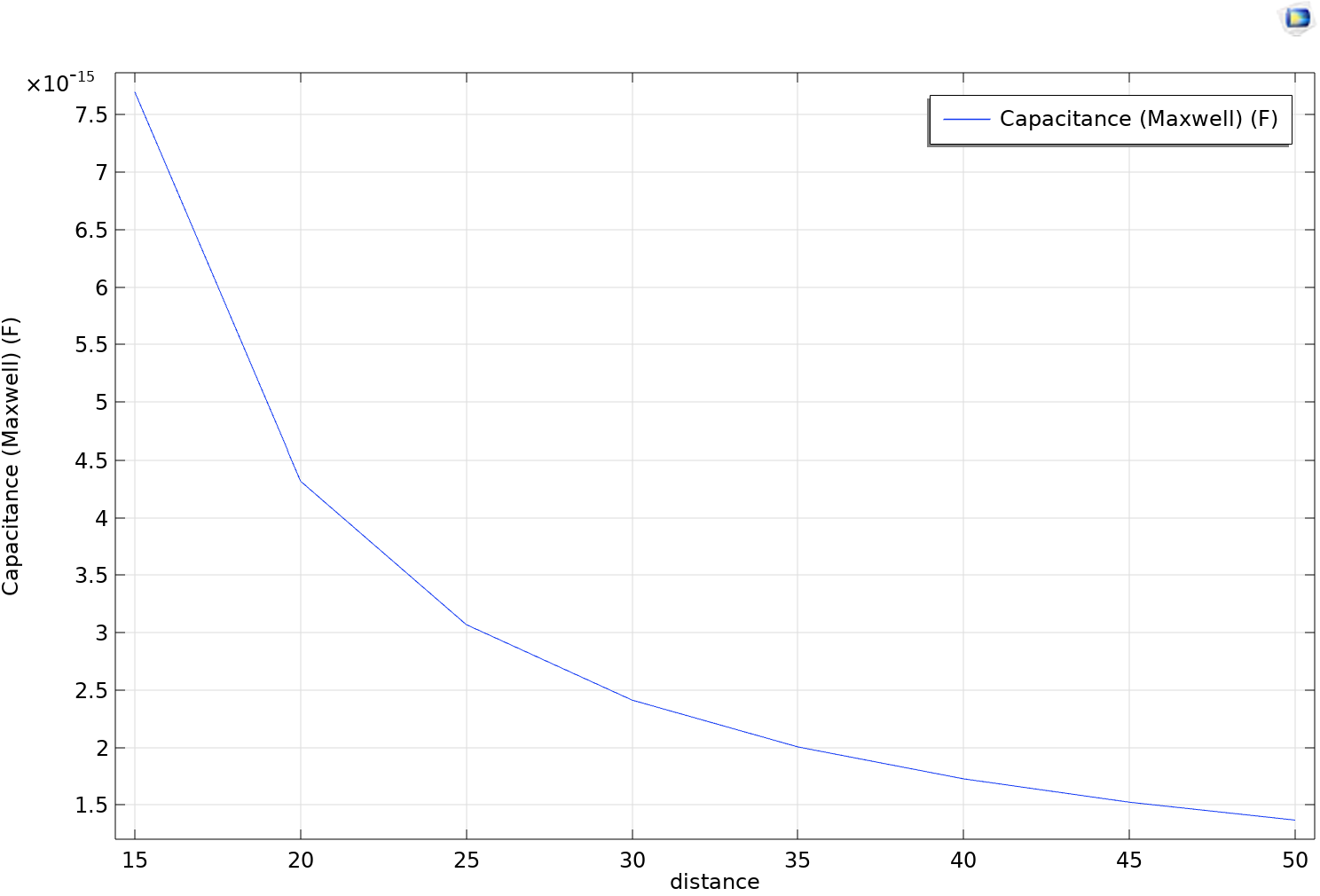
La présence des 2 autres électrodes ne semble pas perturber significativement le système pour la détermination de la distance de la main à l'électrode.
3.2 - Conception du conditionneur
La conception du conditionneur se divise en plusieurs parties distinctes :
- Un circuit permettant de charger la capacité avec un courant constant.
- Un oscillateur avec un comparateur à hysteresis.
La méthode pour déterminer la capacité consiste à charger un condensateur (ici le condensateur est formé par la main de l'utilisateur et l'électrode reliée au circuit conditionneur) à courant constant. On peut ainsi déterminer la capacité en fonction du temps de charge.
3.2.1 - Charge d’un condensateur à courant constant
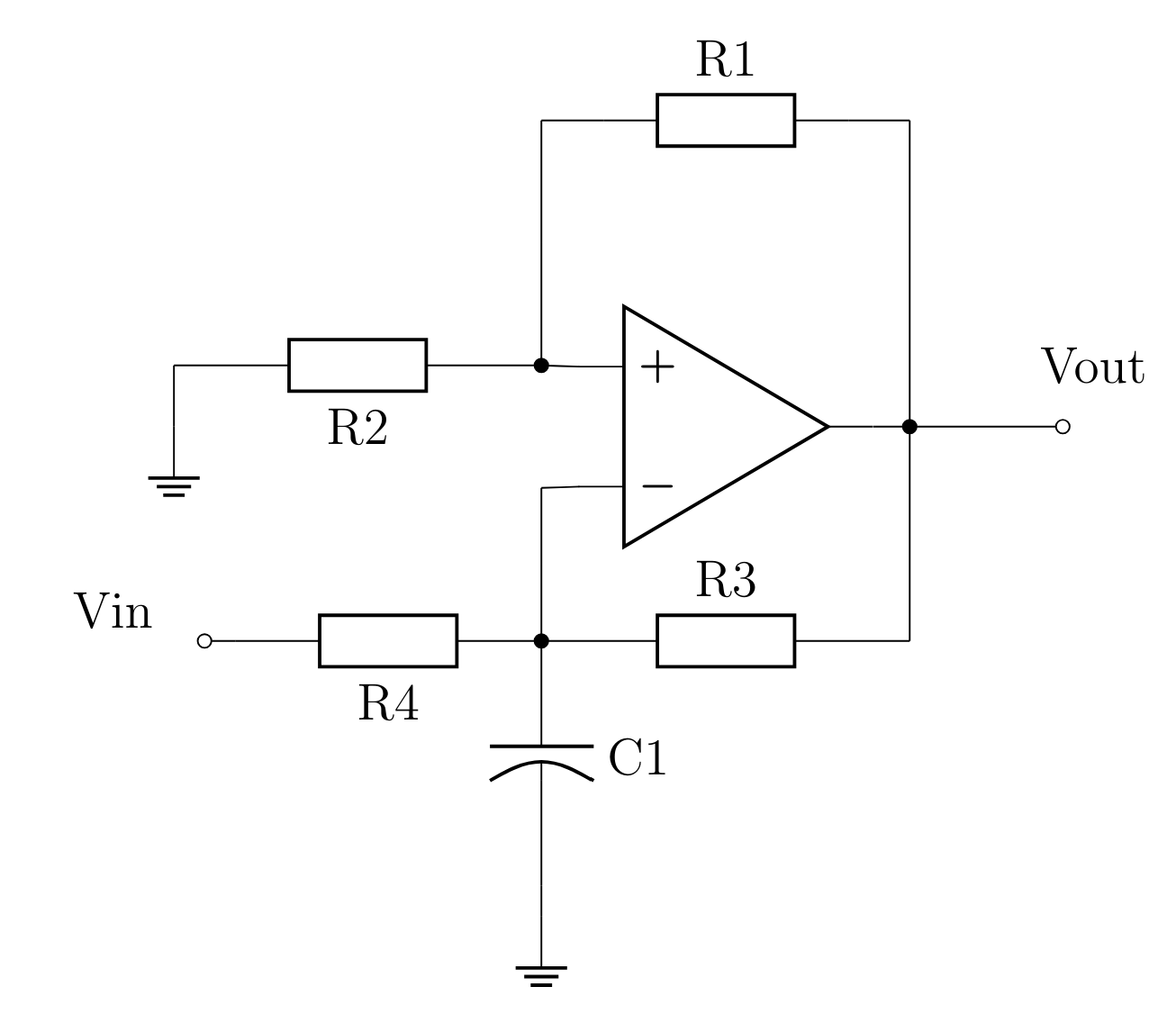
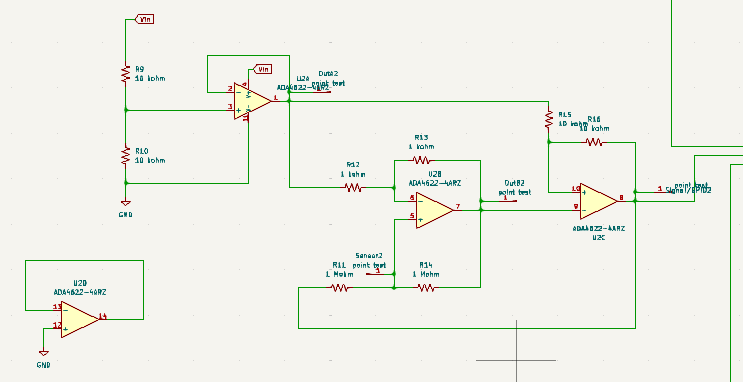
Le circuit permet de fournir un courant constant à la capacité C1. La tension de charge devient donc une fonction linéaire, cela permet de relier directement la valeur de la capacité à fréquence d'oscillation du circuit qui dépend du temps de charge du condensateur.
Le courant que le condensateur reçoit est \(i = \frac{Vin}{R_4}\) Sur PartQuest on modélise le circuit permettant la charge du condensateur à courant constant.
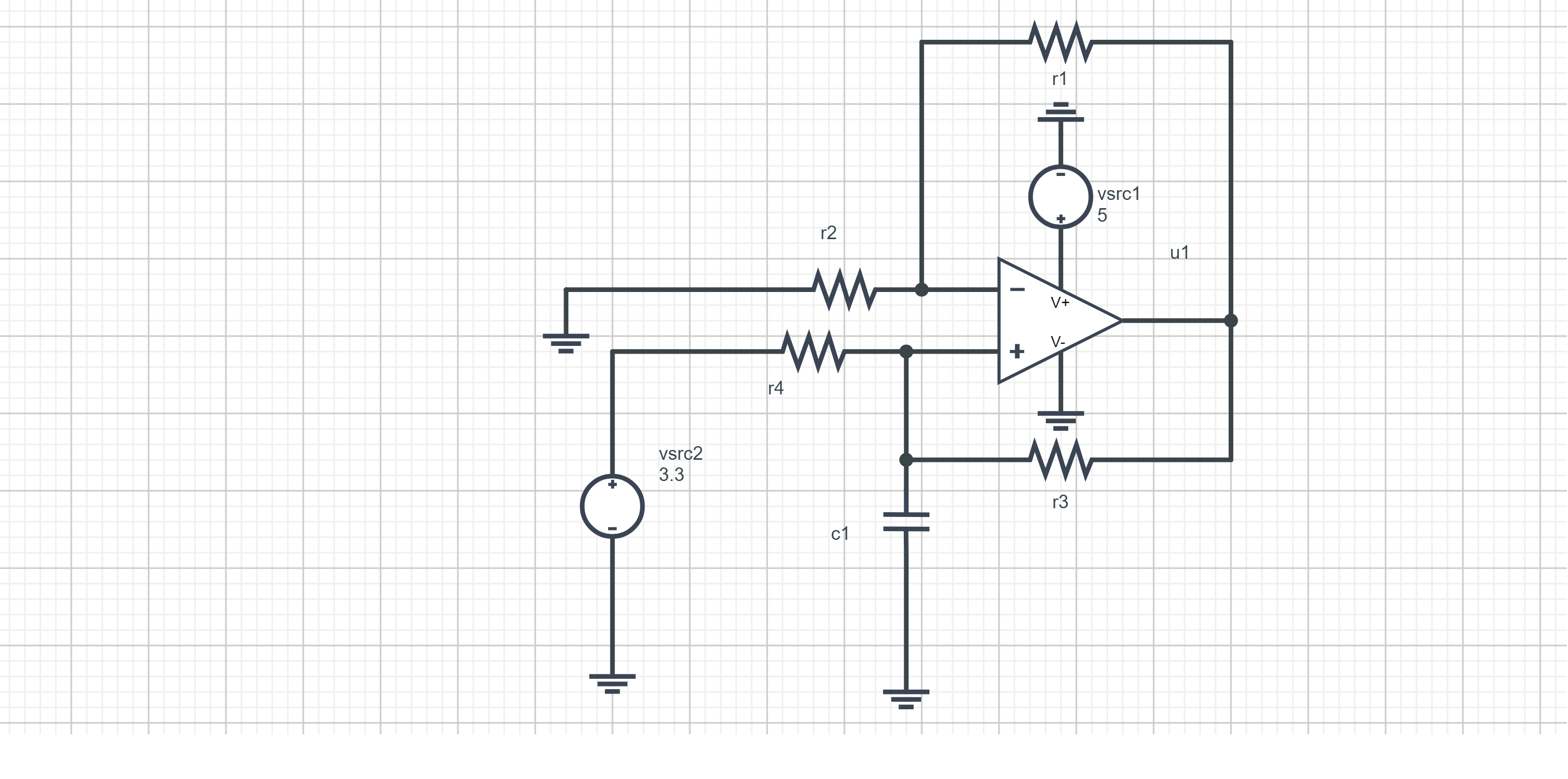
On fixe R1 = R2 = 1 M\textOmega. D'autre part R3 = R4 = nR1 = nR2. Ici on a pris n = 4 tel quel que R3 = R4 = 4 M\textOmega. On prend C1 = 10 pF. L'AOP est alimenté asymétriquement en 0V et 5V. Vin est fixé à 3.3 V.
On obtient alors la simulation suivante :
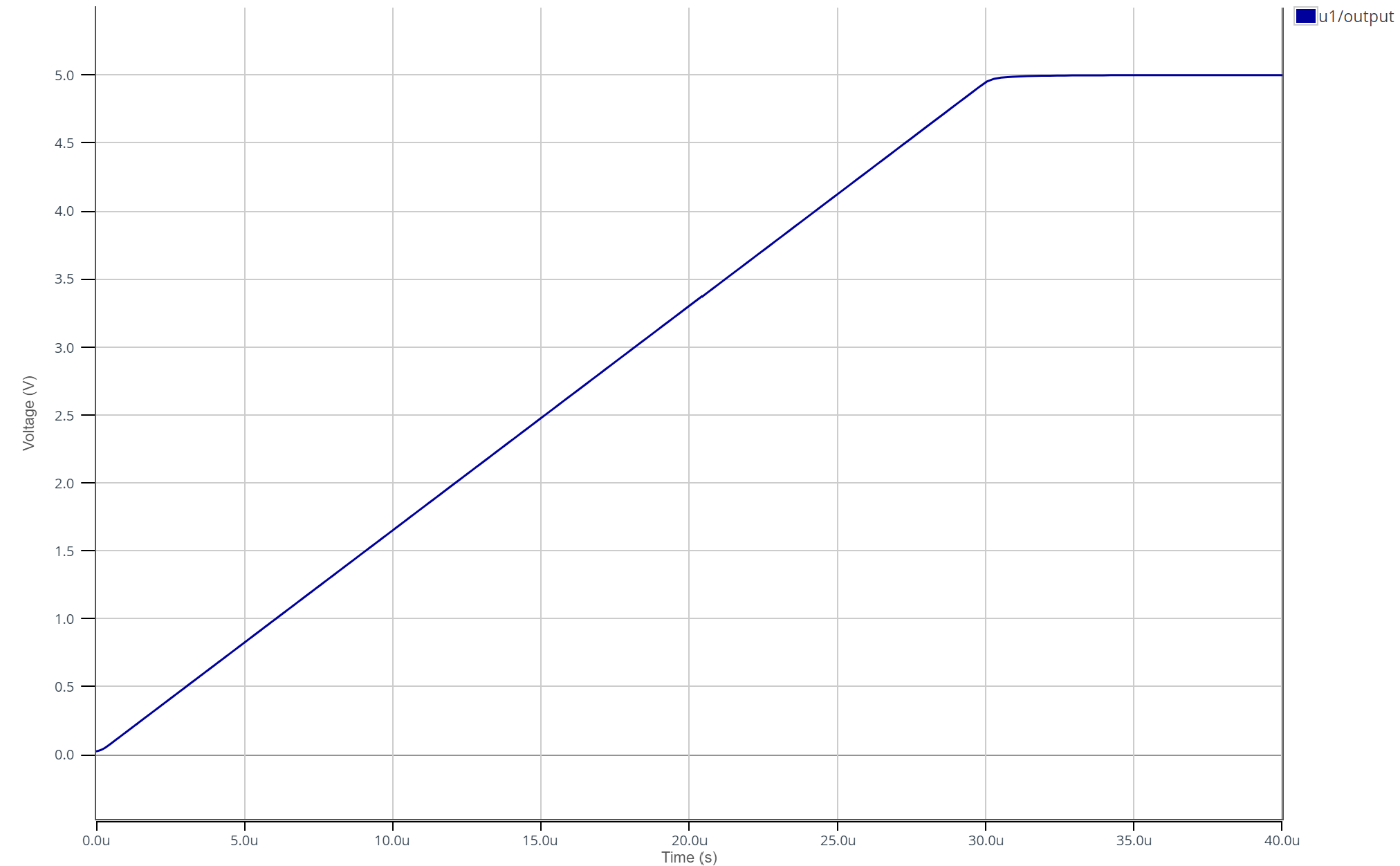
On observe une saturation en tension à 5V correspondant à l'alimentation de l'AOP. On observe d'autre part une charge linéaire du condensateur.
L'équation régissant le fonctionnement d'un condensateur est \(i_C = C\frac{d u_C}{dt}\). On mesure une pente \(\frac{d u_C}{dt} = 1.6\cdot 10^5 \text{ V/s}\). Sachant que le courant de charge est de 8.25e-7 A on détermine la capacité \(C1= \frac{\frac{du_{C}}{dt}}{i_c} = \frac{1.6\cdot 10^5}{8.25\cdot 10^{-7}} = 5.5\text{ pF}\).
3.2.2 - Comparateur à hysteresis
Il est ensuite nécessaire de concevoir le comparateur à hysteresis afin de detecter le seuil de déclenchement pour le fonctionnemnt en boucle fermée.
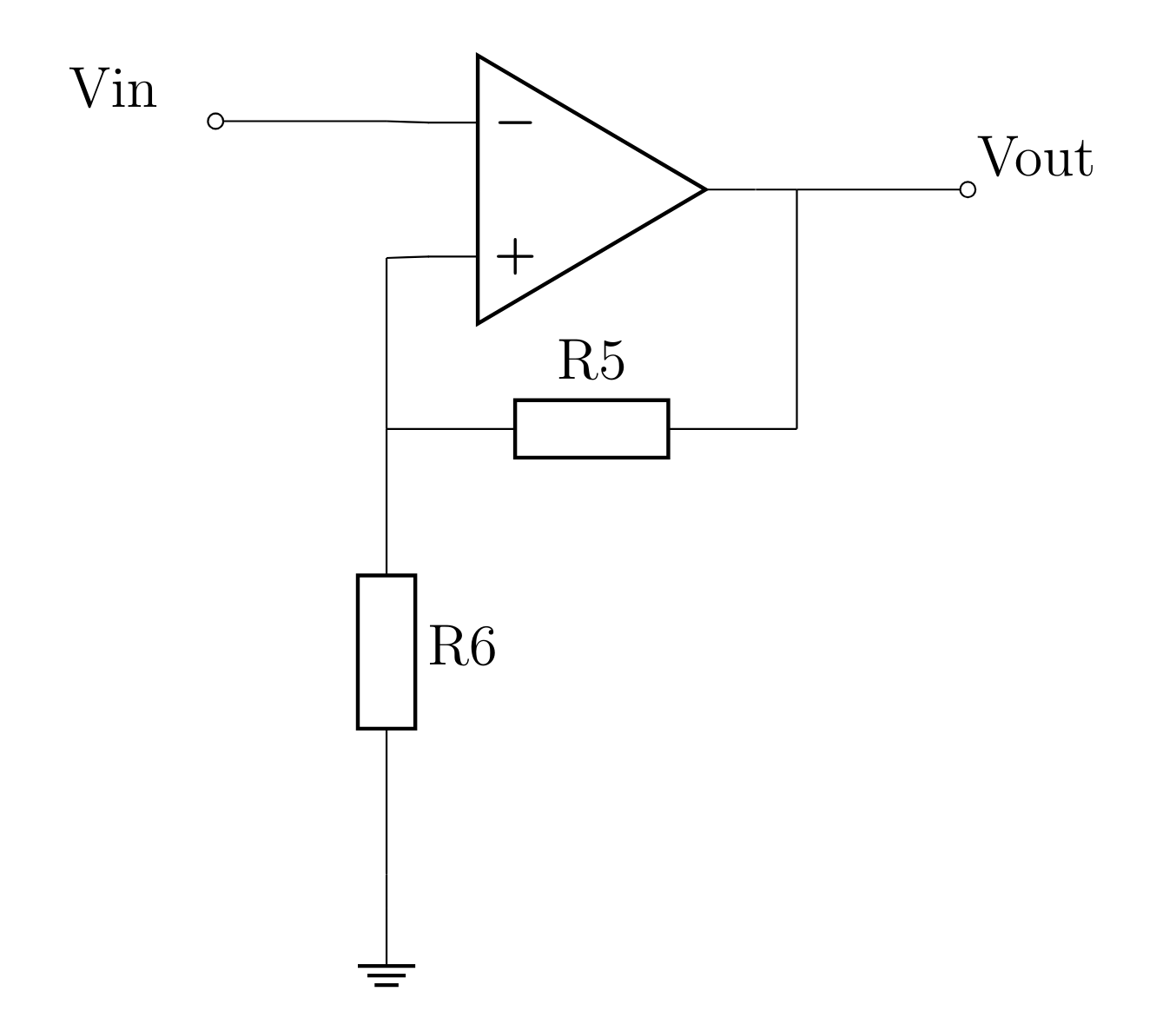
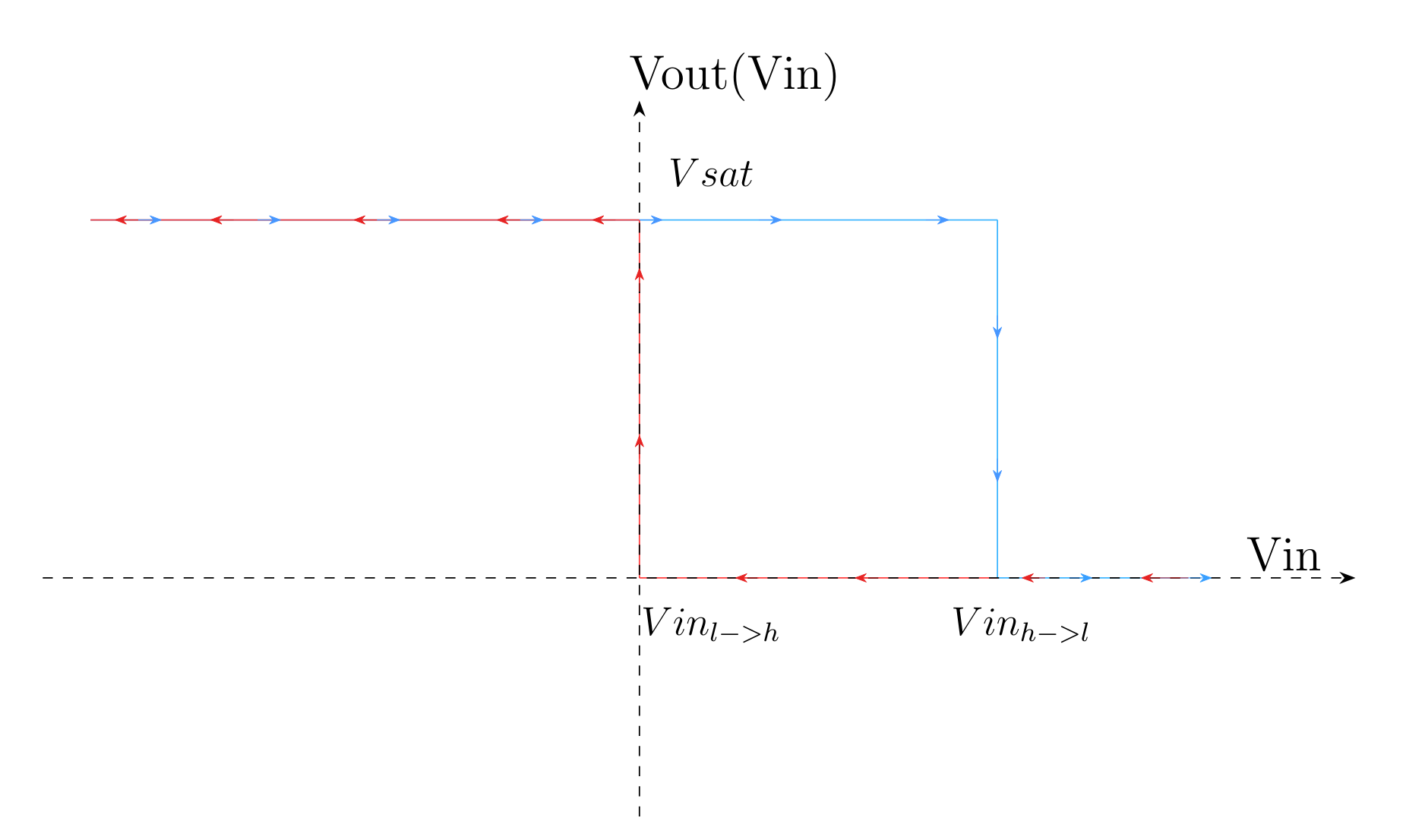
\(Vin_{l->h} \text{ et } Vin_{h->l}\) représentent respectivement les seuils de basculement de 0 V à Vsat et Vsat à 0 V. Ici Vsat = 5V et correspond à la tension d'alimentation de l'AOP.
On montre alors que \(Vin_{h->l} = \frac{R_{6}}{R_{5} + R_{6}} Vsat\) et \(Vin_{l->h} = 0\). Les démonstrations sont à la section 7.2 - Démonstrations
3.2.3 - Simulation du circuit en boucle fermée
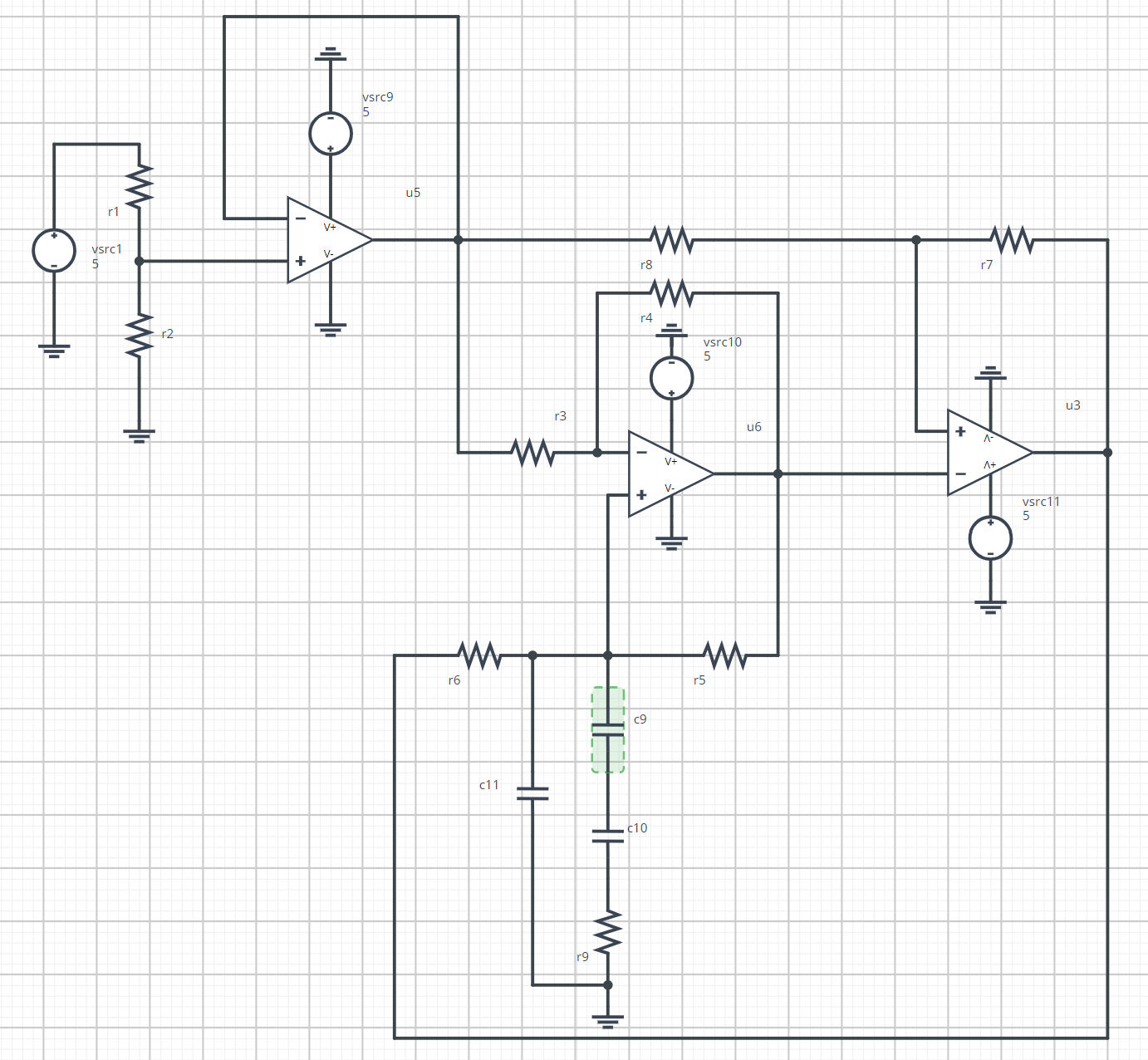
On effectue la simulation en faisant varier la distance entre l'électrode et la main entre 1mm et 10 cm :
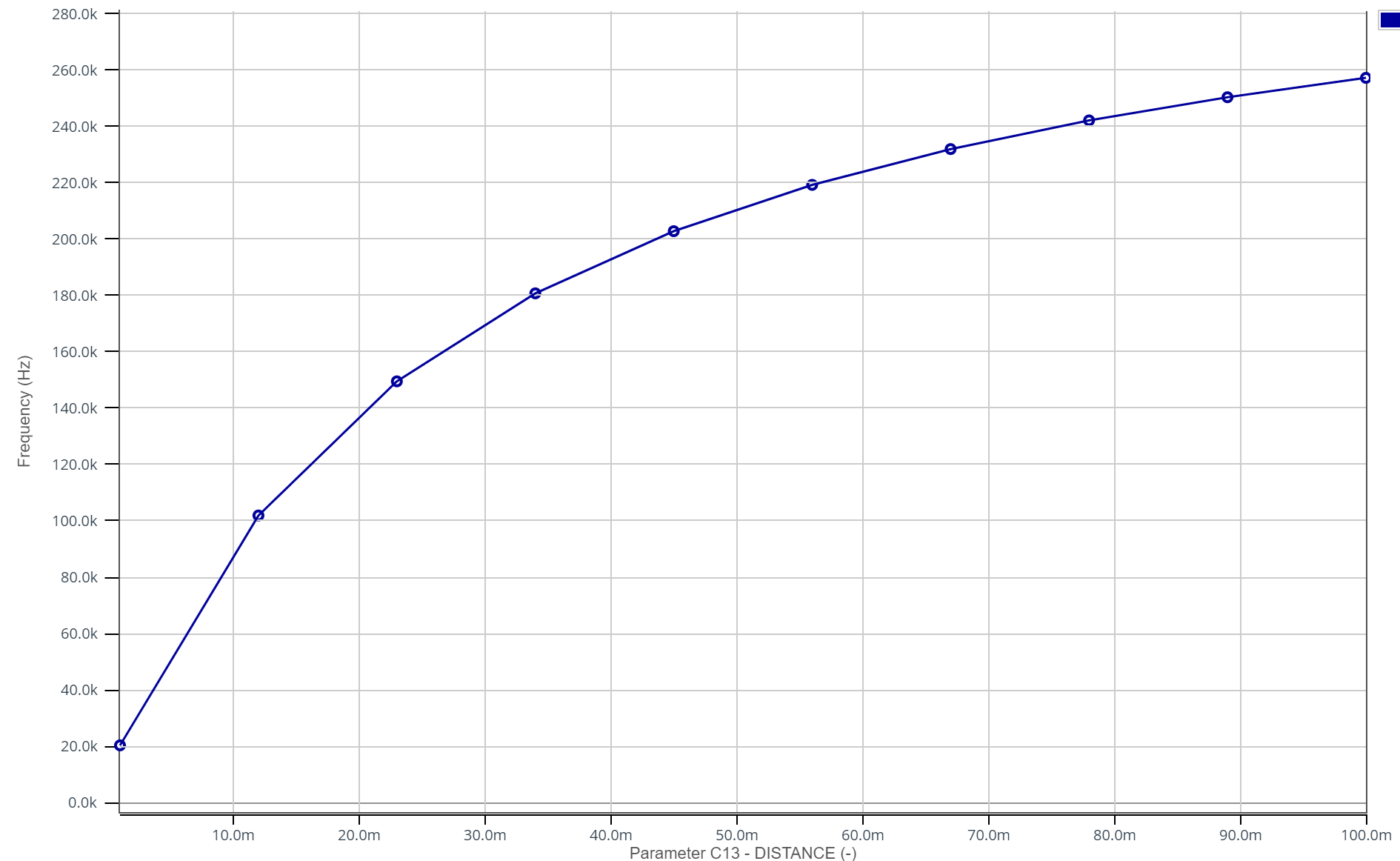
3.3 - Conception du PCB sous KiCAD
La conception du PCB a été réalisée en deux étapes. Tout d'abord, nous avons conçu le circuit complet de notre projet, comportant une STM32 principale reliée à trois conditionneurs en entrée, ainsi qu'une LED RGB, un bouton et une sortie point test. Dans un premier temps, nous avons routé l'ensemble du projet sur un seul et même PCB (les trois conditionneurs, la STM32 et l'ensemble des sorties).
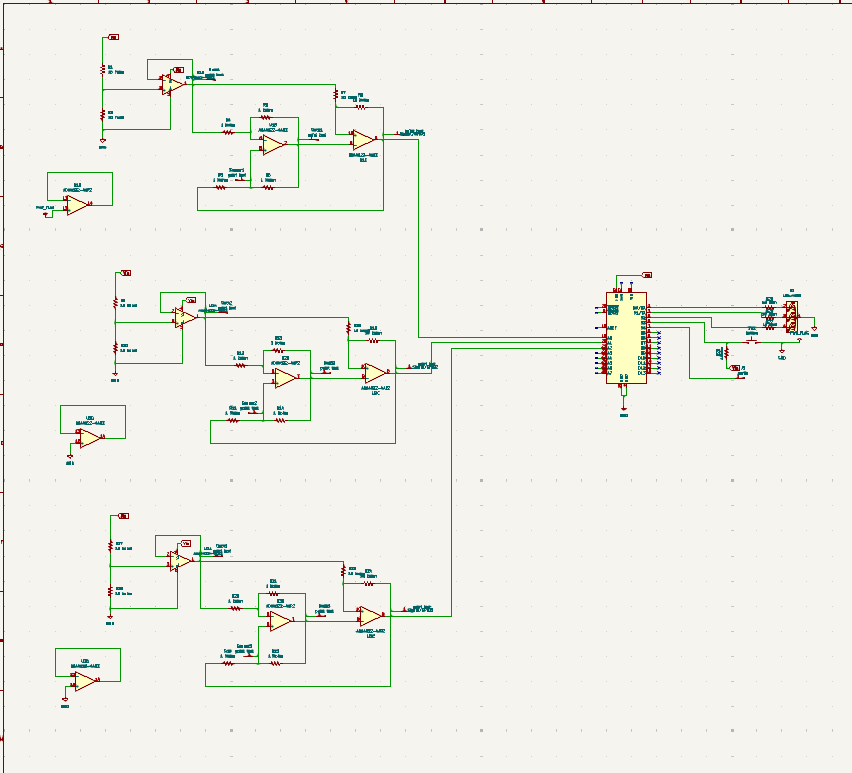
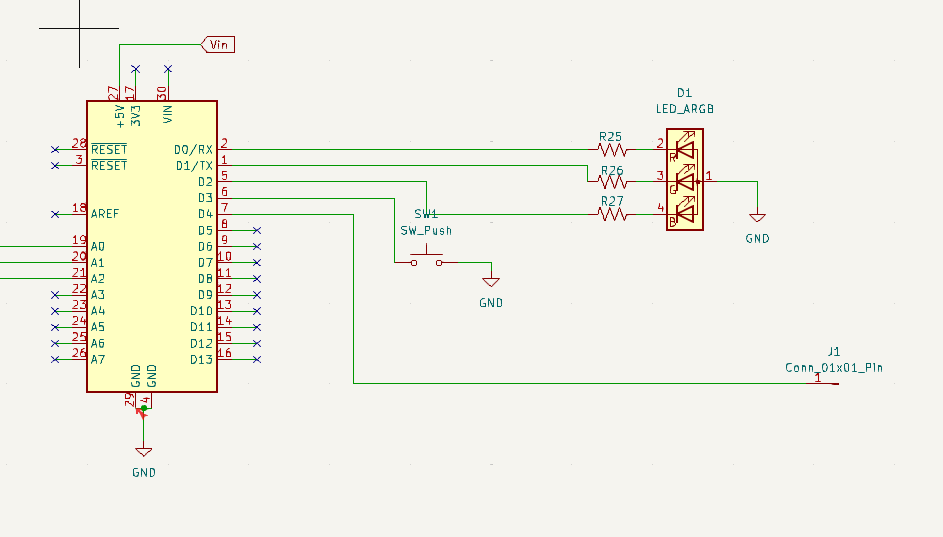
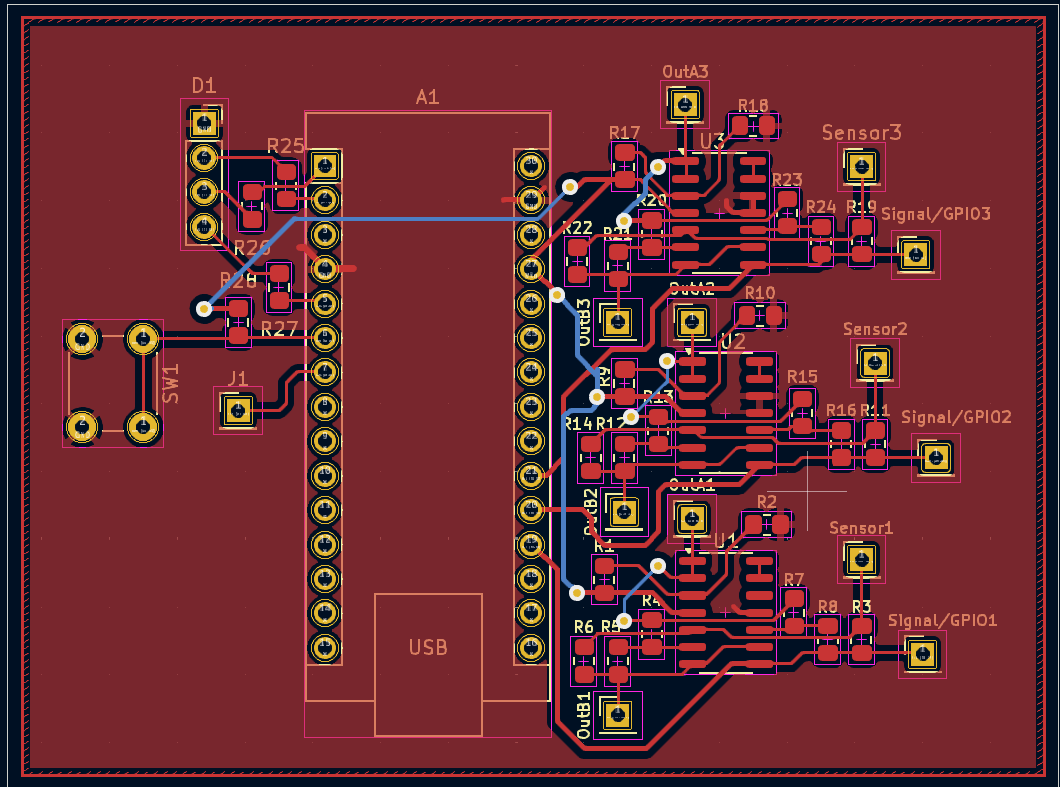
Mais, en raison d'un manque d'AOP, il nous a été déconseillé d'imprimer notre PCB et de souder l'ensemble. On nous a alors encouragés à refaire notre routage en intégrant directement des conditionneurs tout faits. Cette méthode permettait de simplifier le processus de développement, d'éviter les erreurs, tout en simplifiant le processus de fabrication.
Nous avons donc décidé de remplacer les conditionneurs par des empreintes de microcontrôleurs STM32, afin de pouvoir utiliser des conditionneurs déjà faits. Dans la continuité de cette optimisation, nous avons également entrepris de remplacer les empreintes de la LED RGB et du bouton, ce qui nous a offert plus de liberté dans le design de notre projet en nous affranchissant des contraintes liées à l'accessibilité de certaines parties du PCB. Nous avons alors repris le routage à zéro.
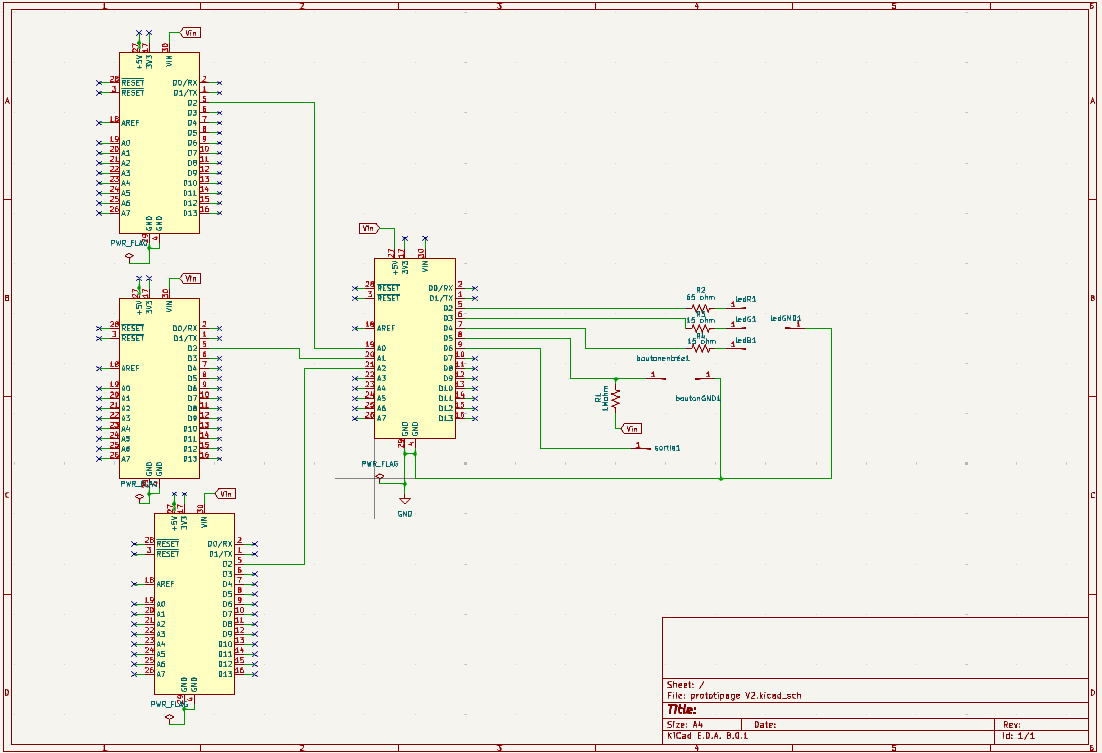
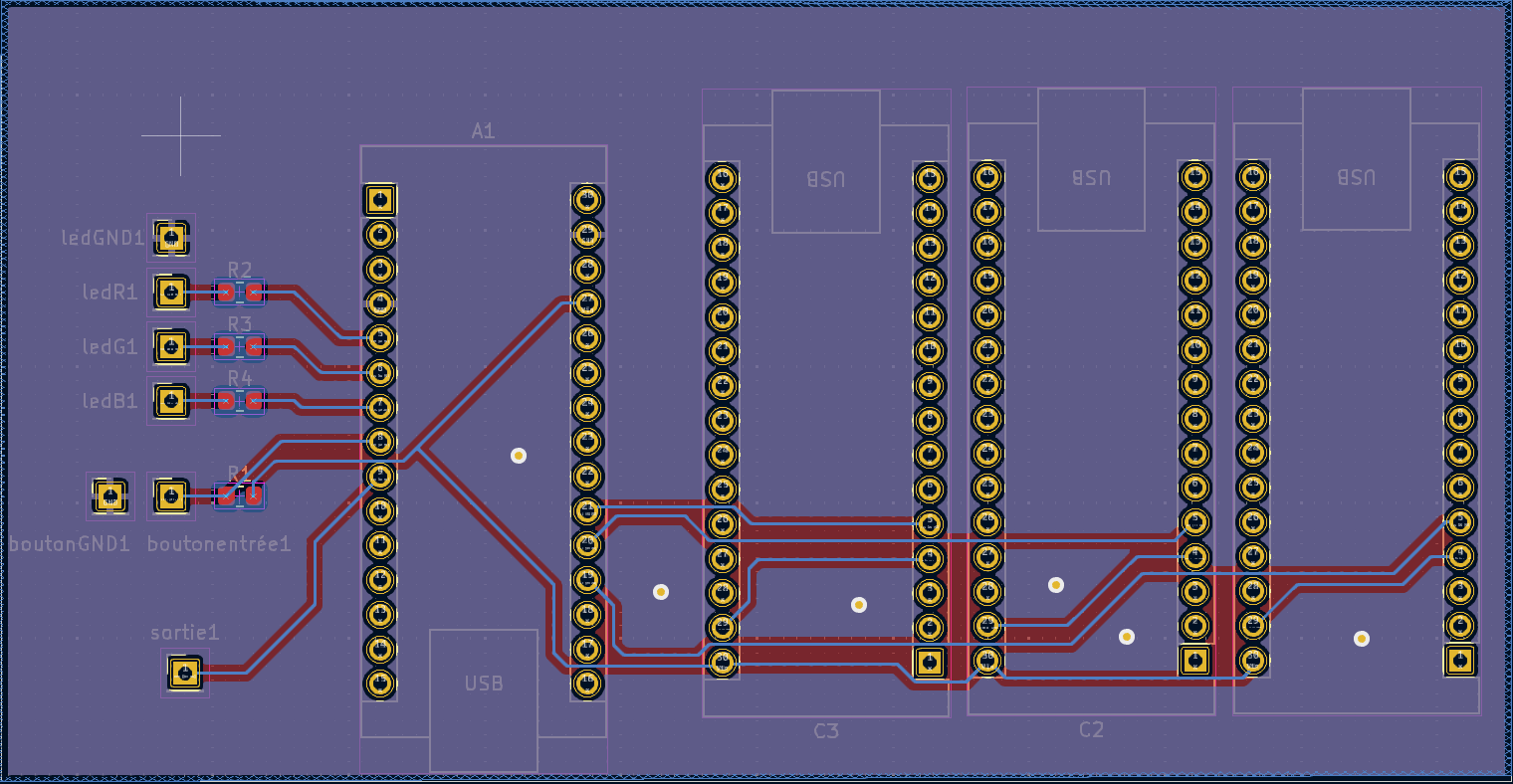
Cette méthode nous a posé de nouveaux problèmes, notamment sur l'orientation des empreintes pour correspondre avec les conditionneurs tout imprimés. Après de nombreuses corrections, nous avons finalement validé notre PCB, qui a été lancé en impression. C'est cette version qui deviendra la base de notre projet de prototypage. Nous avons également fait face à un manque de conditionneurs et avons finalement dû en router deux nous-mêmes. Cette méthode nous a fait perdre beaucoup de temps et a repoussé nos phases de test, car en l'absence de PCB et de conditionneurs, l'avancement de notre projet était limité.
3.4 - Tests et mesures
Après assemblage de notre conditionneur, on peut tester le changement de fréquence en sortie du circuit.
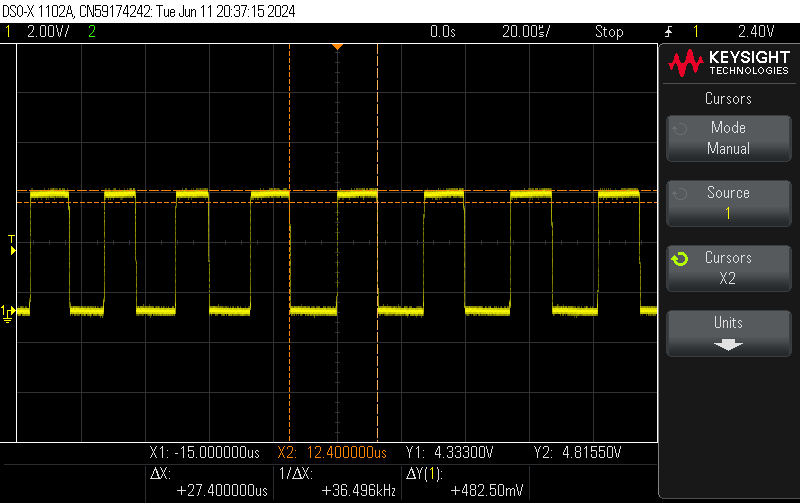
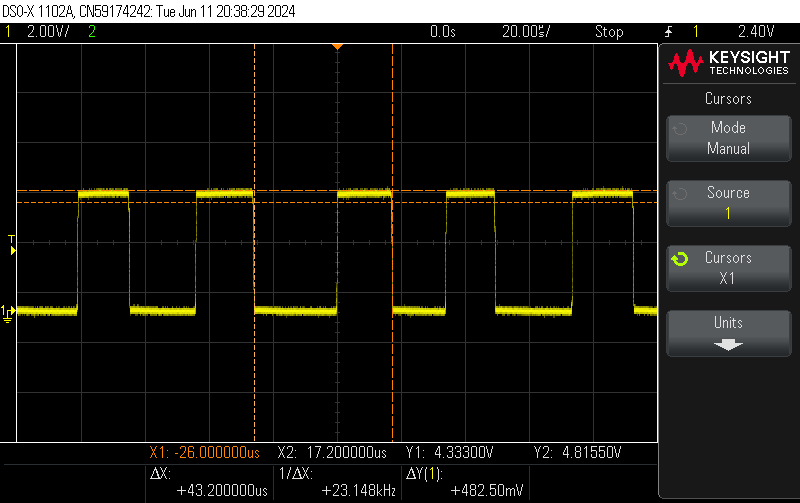
On constate que sans main à proximité, la fréquence est de 36 kHz alors que lorsqu'on approche la main de la plaque de cuivre, la fréquence diminue pour atteindre ici par exemple, 23 kHz.
La fréquence à donc bien diminuée comme attendu lors de l'approche de la main du la plaque de cuivre.
4 - Acquisition du signal avec un microcontrôleur STM32
4.1 - Architecture globale du code d'acquisition
Afin d'acquérir le signal on utilise le microcontroleur STM32. Pour déterminer la fréquence on utilise un timer qui mesure le temps entre deux fronts montants à l'aide d'une interruption. On détermine ainsi la fréquence puis la capacité à l'aide de la relation \(f = \frac{1}{RC}\), avec R = 1 M \Omega.
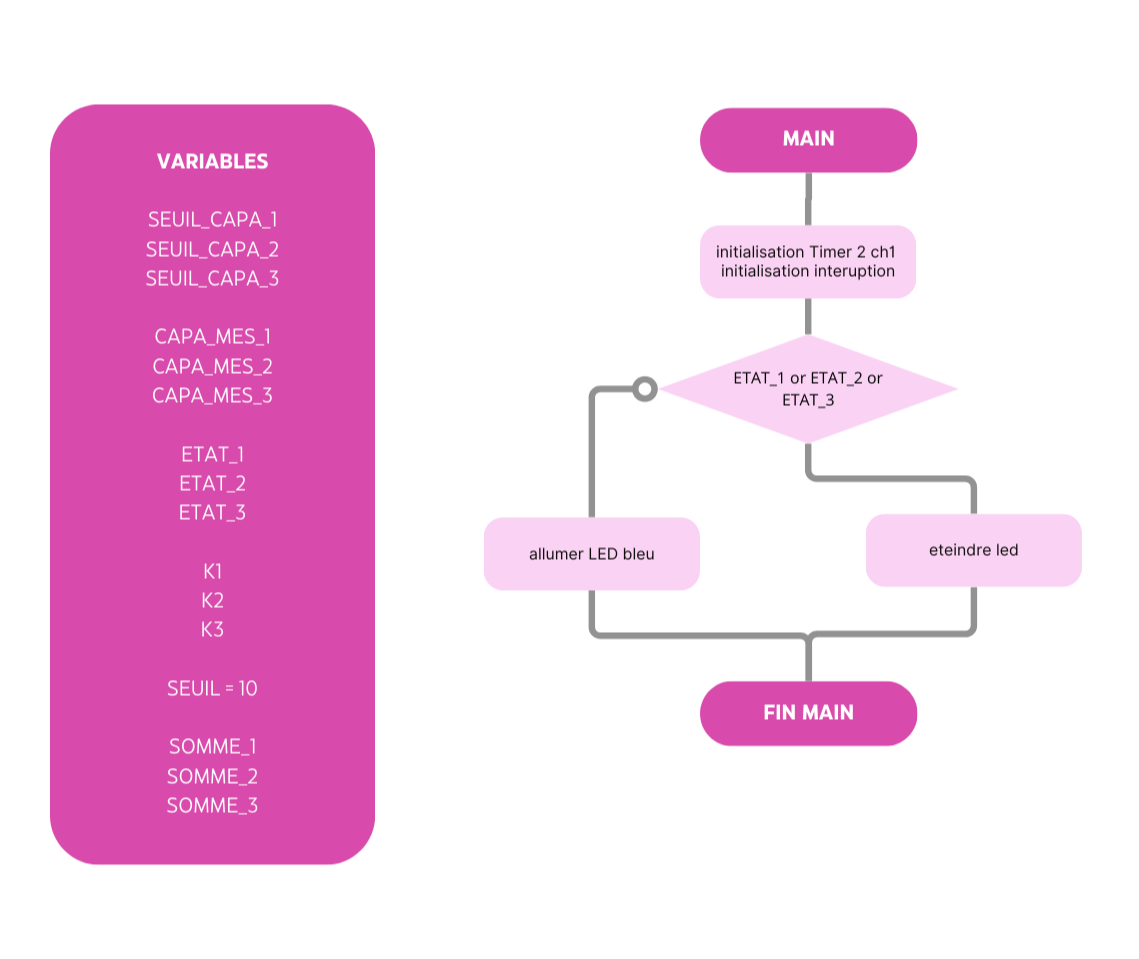
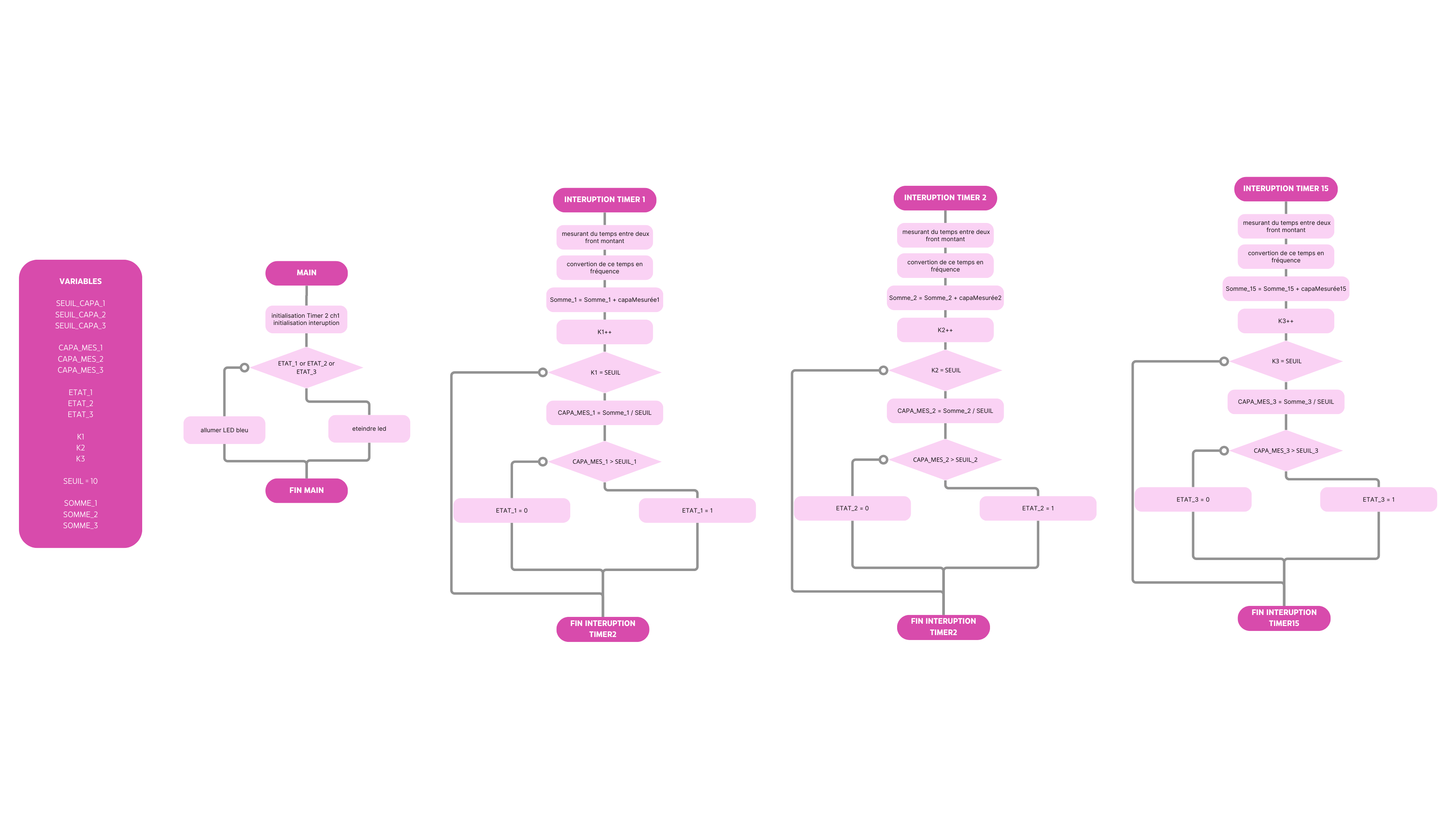
Pour plus de précision, on peut se référer au diagramme suivant qui détaille l'acquisition de la fréquence/capacité à l'aide du timer :
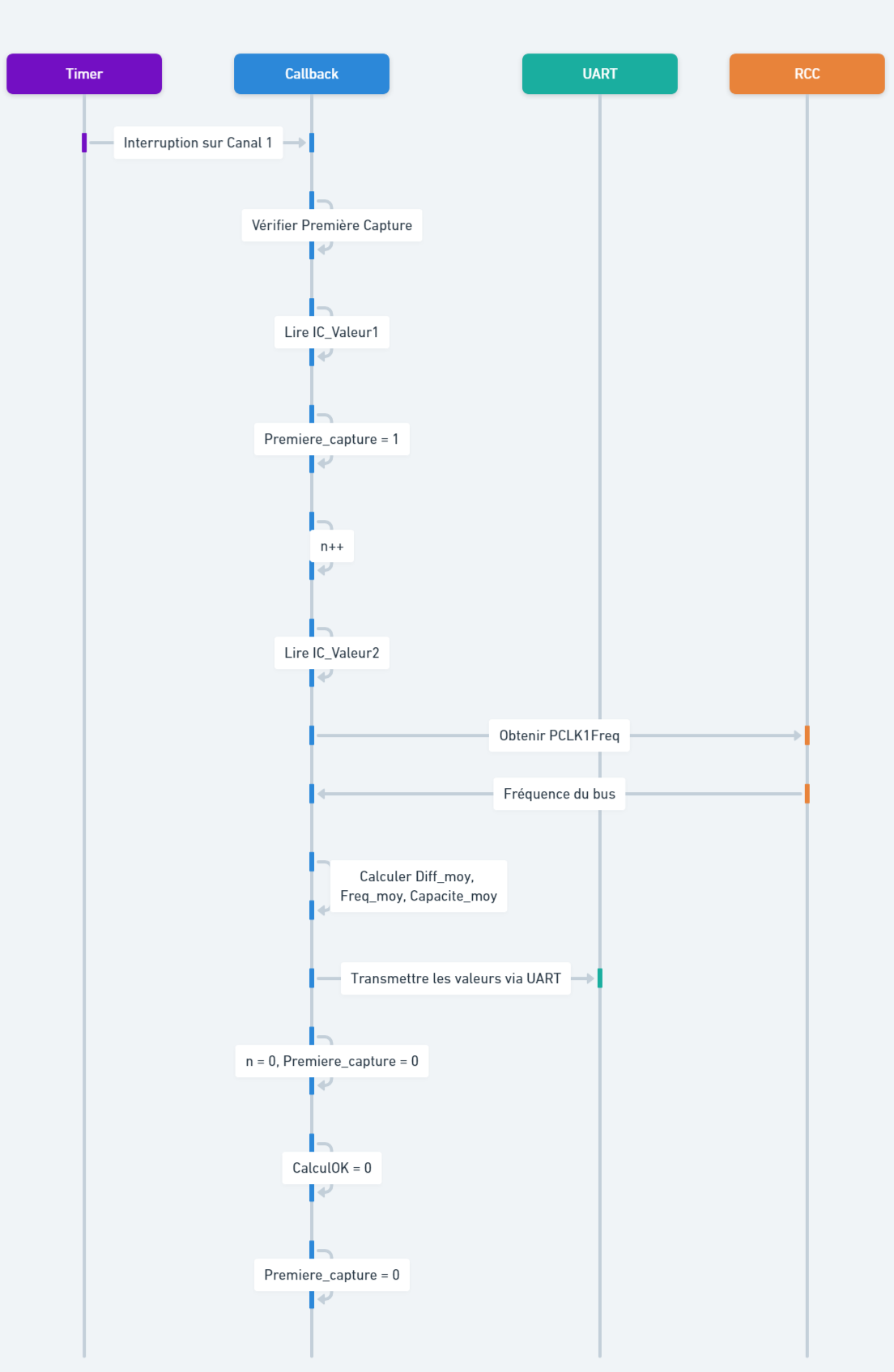
Pour la conception nous avons utilisé une transmission UART afin de visualiser les valeur de notre capacité. Cependant nous avons rencontré plusieurs problèmes. La carte STM32 F301K8 est une "MCU selector" et non une "Board selector", cela nous a empeché de voir certaines connexions, notamment celle de l'UART1 qui est utilisé pour le ST-LINK. Nous avons donc été bloqués car le UART1 était inutilisable. Nous avons donc au bout de quelques recherches trouvé qu'il fallait utiliser l'UART2 pour transmettre les données.
On n'utilisons pas de prescalaire, et nous mettrons l'ARR à une très grande valeur (8000000). Nous avons activé l'option 'NVIC', pour l'interruption pour la fonction Callback.
4.2 - Détails techniques de l'acquisition de signal
5 - Finalisation du projet
5.1 - Tests et mesures du système
Après avoir programmé le microcontrôleur, nous avons relevé plusieurs mesures caractérisant le bon fonctionnement de notre système.
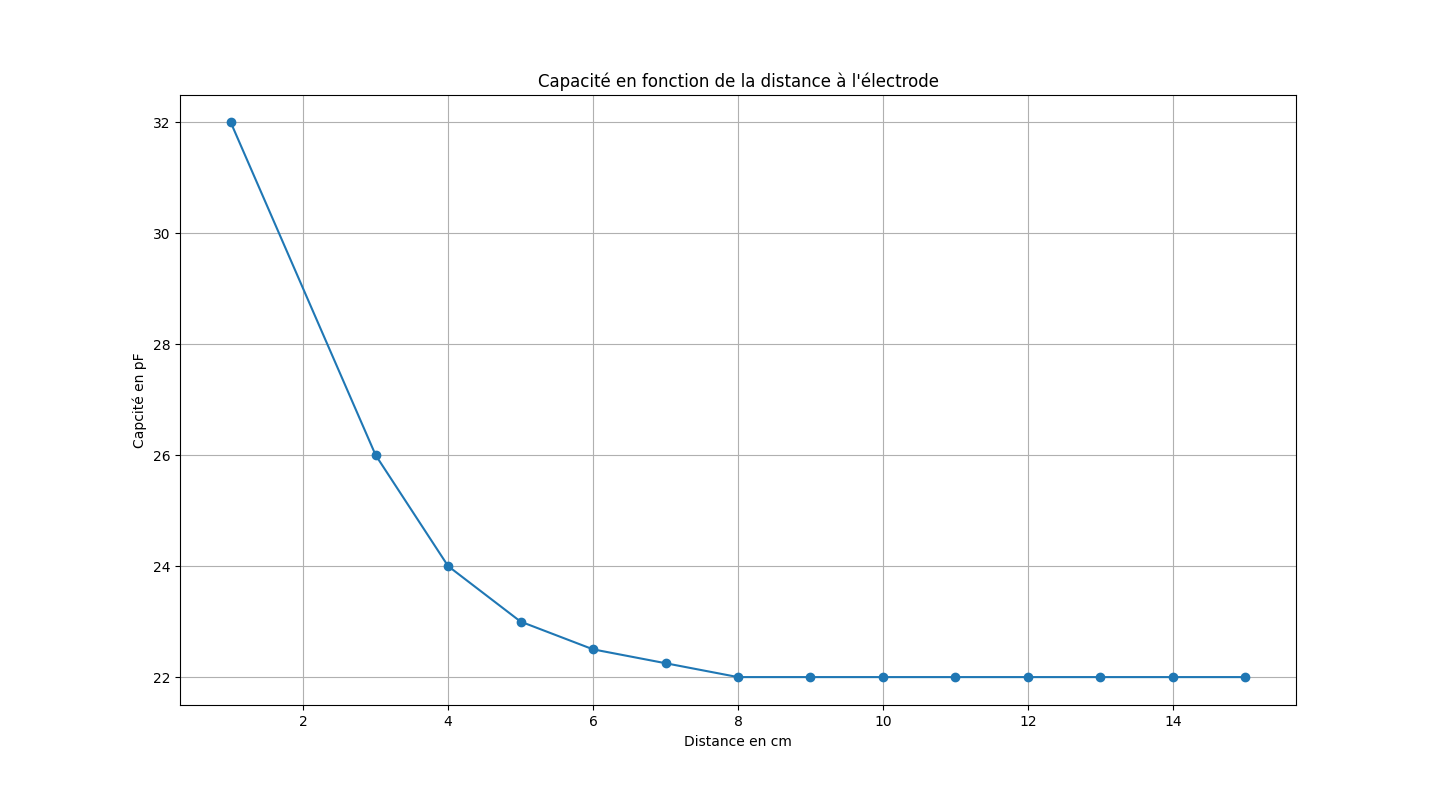
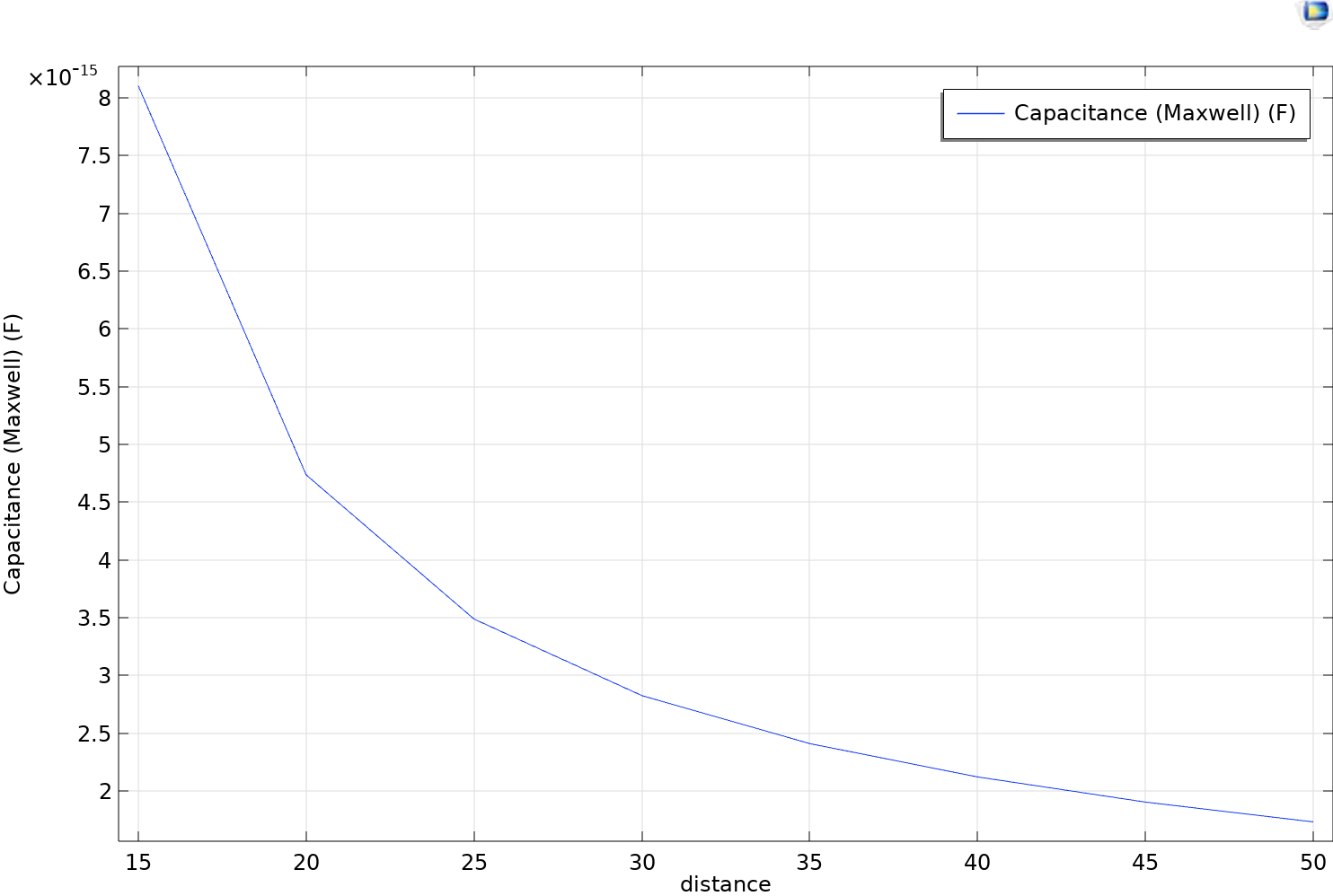
Nous avons relevé la capacité mesurée à intervalle régulier puis nous l'avons tracé en fonction de la distance. Nous constatons alors que l'allure ainsi que les valeurs sont cohérentes avec celles théoriques.
On remarque que au-delà de 8 cm, la variation de capacité est quasi nulle, ce qui rend toute mesure imprécise. On veillera donc à ne pas dépasser cette valeur pour la mise en place du seuil de détection pour les 2 positions de la main au dessus de l'électrode. Plus le seuil est proche de 0 cm, plus le système sera précis mais plus il est compliqué pour l'utilisateur de positionner correctement sa main dans les 2 positions : il s'agit alors de trouver un compromis entre précision et ergonomie.
On détecte 2 positions pour la main : proche ou éloignée :


La couleur de la led permet à l'utilisateur de bien positionner sa main à la bonne distance de l'électrode afin de "rentrer" le bon code souhaité.
Ce système fonctionne pour les 3 électrodes permettant d'entrer le code souhaité et ainsi d'effectuer l'action demandée.
Afin d'être sûr de la position de la main, plusieurs mesures sont effectuées par le microcontrôleur avant d'allumer la led de la bonne couleur. Cela permet de réduire le nombre d'erreurs et ainsi d'améliorer la précision du système.
5.2 - Fabrication finale

Nous avons modéliser un boîtier imprimé en 3d permettant de contenir le microcontrôleur ainsi que les 3 conditionneurs pour les 3 électrodes.
La led RGB se situe sur le dessus et s'allume pour avertir l'utilisateur de la bonne position de sa main ou non.
Enfin, notre actionneur est ici un servomoteur qui ouvre une petite porte qui pourrait être en vrai une plus grosse porte pour accéder à un endroit sensible par exemple.
6 - Conclusion et perspectives d'amélioration
Pour conclure, les objectifs fixés au début de notre projet n'ont pas tous pu être atteints, mais nous avons tout de même réalisé des avancées significatives. Malheureusement, l'objectif de sécurité n'a pas pu être pleinement abordé en raison des difficultés techniques rencontrées lors de la fabrication du PCB et de l'élaboration du code. Ces obstacles nous ont empêchés de traiter ce sujet crucial.
Cependant, notre conditionneur a permis d'éviter le contact physique, ce qui assure une bonne hygiène. Néanmoins, cet aspect pourrait encore être amélioré. En optimisant le conditionneur, nous pourrions augmenter la distance entre la main et la plaque de cuivre, offrant ainsi une meilleure protection et confort pour les utilisateurs.
En outre, la simplicité ergonomique de notre projet a pleinement respecté notre souhait d'intuitivité. Cette approche a facilité l'utilisation de notre dispositif, rendant les interactions plus naturelles et accessibles pour tous. Nous restons convaincus que ces bases solides nous permettront de surmonter les défis rencontrés et d'apporter des améliorations futures pour atteindre tous les objectifs initiaux.
Les perspectives pour ce système incluent plusieurs améliorations potentielles. Premièrement, l'optimisation du conditionneur et de la gestion des signaux pourrait améliorer encore davantage la précision et la fiabilité du système.
Deuxièmement, l'intégration d'une interface utilisateur plus intuitive pourrait faciliter l'utilisation du digicode.
Enfin, l'expansion de ce système à d'autres applications de sécurité et d'accès pourrait élargir son champ d'utilisation et le rendre plus polyvalent dans divers contextes.
7 - Annexes
7.1 - Code annexes
7.2 - Démonstration
Expression de la capacité d'un condensateur plan
Symétrie du champ électrique : Pour un condensateur plan infini, les plaques sont infinies et chargées uniformément. Cela implique que le champ électrique \(\vec{E}\) doit être orthogonal aux plaques et uniforme entre elles en raison de l'invariance par translation dans les directions orthogonales aux plaques. La loi de Gauss est donnée par : \[ \iint_{\Sigma} \vec{E} \cdot \vec{dS} = \frac{Q_{int}}{\epsilon} \] Pour appliquer cette loi, considérons une surface gaussienne en forme de cylindre traversant les deux plaques, où les extrémités du cylindre sont parallèles aux plaques du condensateur. La symétrie du problème nous dit que le champ électrique est constant et perpendiculaire aux plaques. Pour une plaque avec une charge superficielle \(\sigma\), la charge totale \(Q_{int}\) incluse dans la surface gaussienne est : \[ Q_{int} = \sigma \cdot S \] où \(S\) est la surface des extrémités du cylindre. Les contributions des parois latérales du cylindre s'annulent, donc l'intégrale de Gauss se réduit aux deux bases du cylindre : \[ E \cdot S + (-E) \cdot (-S) = \frac{\sigma \cdot S}{\epsilon} \] \[ 2ES = \frac{\sigma S}{\epsilon} \] \[ E = \frac{\sigma}{2\epsilon} \] Calcul de la différence de potentiel La différence de potentiel \(V\) entre les deux plaques séparées par une distance \(d\) est donnée par l'intégrale du champ électrique sur cette distance : \[ V = \int_{0}^{d} E \, dx = E \cdot d \] En utilisant la densité de charge \(\sigma = \frac{Q}{S}\), où \(S\) est la surface d'une plaque, nous obtenons : \[ V = \left(\frac{\sigma}{\epsilon}\right) \cdot d = \frac{Q}{\epsilon S} \cdot d \] Détermination de la capacité La capacité \(C\) d'un condensateur est définie par la relation entre la charge \(Q\) et la différence de potentiel \(V\) : \[ C = \frac{Q}{V} \] En substituant l'expression de \(V\) que nous avons trouvée : \[ C = \frac{Q}{\frac{Qd}{\epsilon S}} = \frac{\epsilon S}{d} \] Nous avons démontré que la capacité d'un condensateur plan infini, avec une distance \(d\) entre les plaques et une surface \(S\), est donnée par : \[ C = \frac{\epsilon S}{d} \]
Générateur de courant constant
D'après le thérorème de Millman : \[V_{-} = V_{out}\frac{R_{1}}{R_{1}+R_{1}}\] \[V_{+} = \frac{\frac{V_{in}}{R_{4}}+\frac{V_{out}}{R_{3}}}{\frac{1}{R_{4}}+\frac{1}{Z_{c}}+\frac{1}{R_{3}}}\] De plus, l'aop fonctionnant en régime linéaire on a \[V_{+} = V_{-}\] Ainsi, \[V_{+} = \frac{\frac{V_{in}}{R_{4}}+\frac{R_{1}+R_{1}}{R_{1}R_{3}}V_{+}}{\frac{1}{R_{4}}+\frac{1}{Z_{c}}+\frac{1}{R_{3}}}\] \[\Leftrightarrow V_{+} = \frac{V_{in}}{R_{4}((\frac{1}{R_{4}}+\frac{1}{Z_{c}}+\frac{1}{R_{3}}))-\frac{{R_{1}+R_{1}}}{R_{1}R_{3}}} \Leftrightarrow V_{+} = \frac{V_{in}}{1+\frac{R_{4}}{Z_{c}d}+\frac{R_{4}}{R_{3}}-\frac{R_{4}(R_{1}+R_{1})}{R_{1}R_{3}}}\] Or, d'après la loi d'Ohm on a : \[i=\frac{V_{+}}{Z_{c}}=\frac{V_{in}}{Z_{c}+R_{4}+\frac{Z_{c}R_{4}}{R_{3}}-\frac{Z_{c}R_{4}(R_{1}+R_{1})}{R_{1}R_{3}}}\] On souahite que le courant i soit indépendant de l'impédance de la capacité, on doit donc necessairement avoir : \[Z_{c}+\frac{R_{4}Z_{c}}{R_{3}}-\frac{Z_{c}R_{4}(R_{1}+R_{1})}{R_{1}R_{3}} = 0\] Il vient donc \[\boxed{i = \frac{V_{in}}{R_{4}}}\]
Cycle d'hystérésis
- Supposons que \(Vout = Vsat \Leftrightarrow \epsilon = V_{+} - V_{-} > 0\). Or, \(V_{-} = Vin\) et par la loi d'Ohm on a \(i = \frac{Vsat-V_{+}}{R5} = \frac{V_{+}}{R6}\), car \(i_{+} = 0\). Donc \(R6(Vsat-V_{+})=R5\cdot V_{+} \Leftrightarrow V_{+}=\frac{R6}{R5+R6}\) Ainsi, \(\epsilon > 0 \Leftrightarrow \frac{R6}{R5+R6}Vsat - Vin > 0 \Leftrightarrow Vin < \frac{R6}{R5+R6}Vsat\). La sortie Vout reste donc à l'état haut tant que \(\epsilon > 0 \) ie \(\boxed{Vin < Vin_{h->l} \text{ avec } Vin_{h->l} = \frac{R6}{R5+R6}Vsat}\)
- Supposons que \(Vout = 0 \Leftrightarrow \epsilon = V_{+} - V_{-} < 0\). \(\epsilon > 0 \Leftrightarrow - Vin > 0 \Leftrightarrow Vin < 0\). La sortie Vout reste donc à l'état haut tant que \(\epsilon > 0 \) ie \(Vin > 0\), donc \(\boxed{Vin_{l->h} = 0}\)