CONCEPTION D'UN CAPTEUR DE LA MESURE DE QUALITÉ DU BÉTON
Conception d’un capteur de mesure en quasi temps réel de la qualité du béton précontraint sur un ouvrage d’art
1 - Introduction
1.1 - Contexte et problématique
Le contrôle des ouvrages d’art en France, réalisé tous les deux ans, ne permet pas une détection précoce ni un suivi continu des défauts structurels. Face à ces limites, un capteur connecté capable de mesurer en quasi temps réel la qualité du béton précontraint constitue une solution innovante. Ce dispositif utiliserait les câbles de précontrainte comme guides d’ondes pour détecter et localiser des défauts tels que l’humidité, les fissures ou la corrosion, tout en mesurant le vieillissement via la constante diélectrique.
1.2 - Objectifs
L’objectif de ce projet est de concevoir un capteur capable de mesurer en quasi temps réel la qualité du béton précontraint et de détecter les défauts structurels des ouvrages d’art.
1.3 - Méthodes et ressources
La conception de ce capteur sera subdivisée en plusieurs étapes :
Modélisation de la ligne de transmission : Cette première étape consiste à adapter le modèle théorique aux spécificités du béton précontraint, en tenant compte de la géométrie des câbles et des propriétés diélectriques. Les simulations des paramètres tels que l’impédance caractéristique et le temps de propagation seront effectuées avec PartQuest.
Détection et classification des défauts : Les défauts tels que l’humidité, les fissures et la corrosion seront modélisés et leurs signatures électriques analysées à partir de mesures de réflectométrie temporelle pour établir un protocole de classification.
Suivi du vieillissement : Une analyse fréquentielle permettra de mesurer l’évolution de la constante diélectrique, utilisée comme indicateur de vieillissement global du béton.
Conception du conditionneur électronique : Un conditionneur sera développé pour traiter les signaux issus de la ligne de transmission. Il intégrera un pont de Wheatstone, un amplificateur et un détecteur de crêtes.
2 - Présentation générale du système
Dans cette partie, nous présenterons les principes généraux de fonctionnement du système, notamment en décrivant ses sous-systèmes.
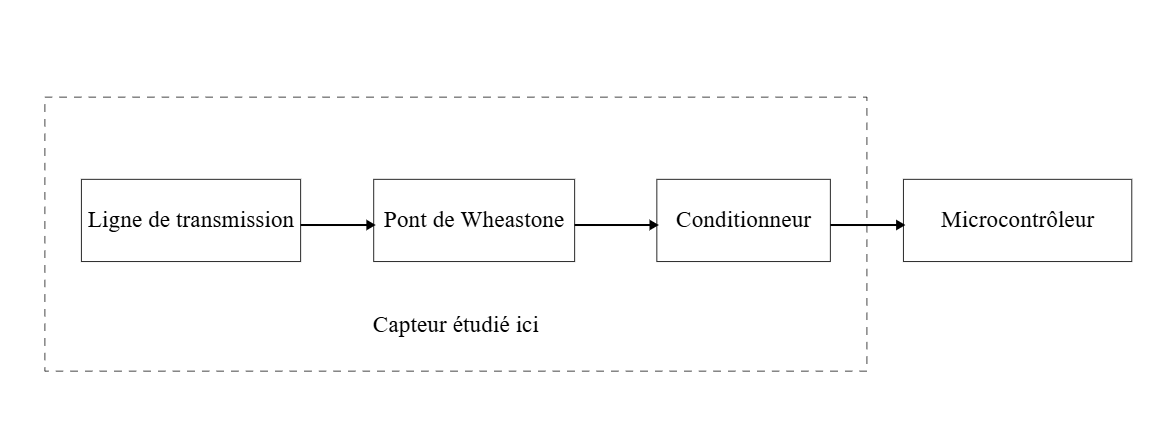
Le système est composé de 3 grands sous-systèmes :
La ligne de transmission : Il s’agit de l’élément sensible du capteur, directement influencée par l’état du béton. Ses propriétés électriques, notamment l’impédance caractéristique, varient en fonction de l’humidité, des fissures ou de la corrosion. Ces variations modifient la propagation des signaux dans la ligne, traduisant les changements physiques du béton en paramètres électriques mesurables.
Pont de Wheatstone : Il est utilisé pour détecter les variations d’impédance de la ligne de transmission en réponse aux défauts dans le béton. Lorsque le béton reste intact, le pont est équilibré et la tension de sortie est nulle. En cas de défaut (humidité, fissure, corrosion), l’impédance de la ligne change, déséquilibrant le pont et générant une tension proportionnelle à la variation. Ce montage permet de convertir le changement d’impédance en tension électrique.
Conditionneur : Il a pour rôle de transformer le signal brut délivré par le pont de Wheatstone, faible et alternatif, en une valeur exploitable par le système de traitement. Il comprend un soustracteur, qui extrait la différence de potentiels, un détecteur de crêtes, qui convertit le signal alternatif en une tension continue, et un amplificateur, qui ajuste le niveau du signal afin de le rendre compatible avec un microcontrôleur.
3 - Différents sous-systèmes
3.1 - Ligne de transmission
3.1.1 - Formalisation de la ligne de transmission
Le but de cette partie est d’établir l’équation d’onde de d’Alembert qui régit la propagation du signal le long de la ligne de transmission.
La ligne est orientée selon l’axe (Ox). On note u(x,t) et u(x+dx,t) la tension entre les deux câbles respectivement à la côte x et d+dx. On note i(x,t) et i(x+dx,t) le courant circulant dans le sens des x croissants respectivement à la côte x et d+dx.
Les grandeurs R, G, L et C sont linéiques. Enfin, on choisit la longueur élémentaire dx suffisamment petite pour que l’ARQS soit valide à l’échelle du tronçon.
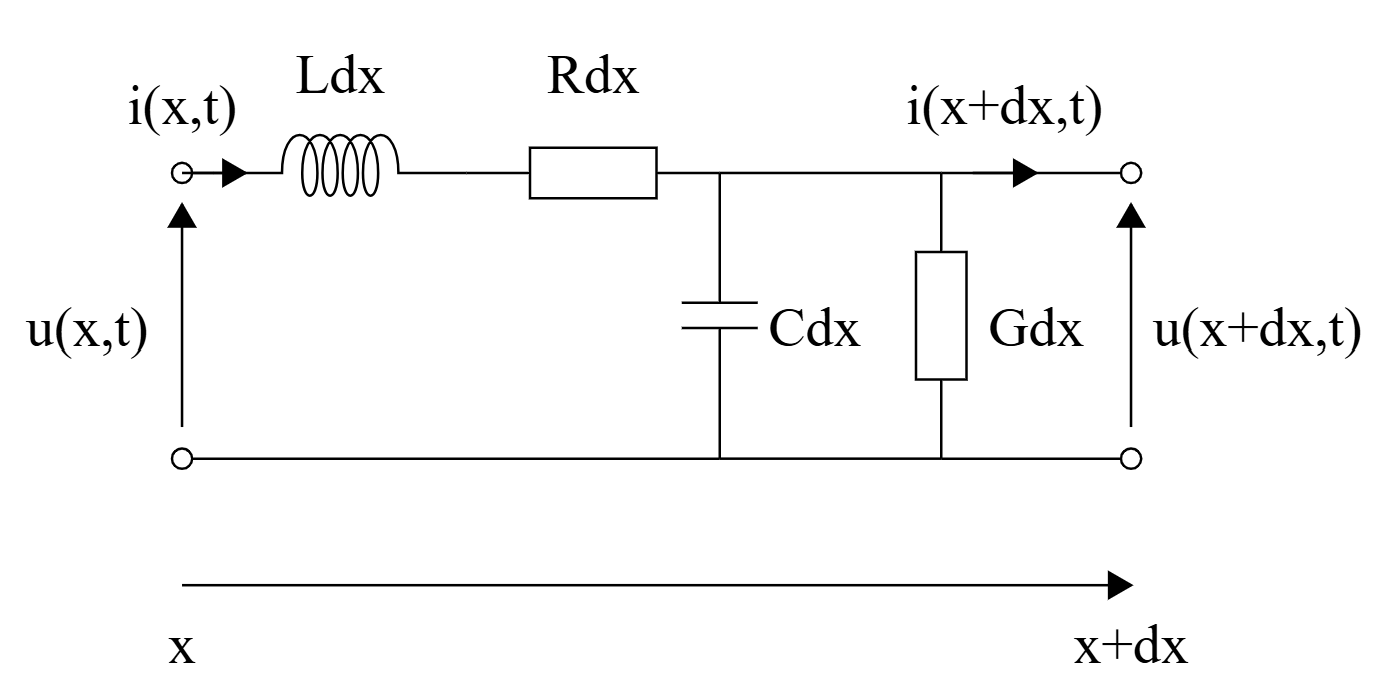
Par application de la loi des noeuds et loi des mailles, on peut montrer que la tension et le courant sont liés par le système d’équations aux dérivées partielles suivantes :
\[\begin{cases} \frac{\partial u}{\partial x}(x, t) = -L \frac{\partial i}{\partial t}(x, t) - R i(x, t), \\ \frac{\partial i}{\partial x}(x, t) = -C \frac{\partial u}{\partial t}(x, t) - G u(x, t) \end{cases}\]
On déduit de ce système l'équation ne faisant intervenir que la tension :
\[ \frac{\partial^2 u}{\partial x^2}(x, t) = L C \frac{\partial^2 u}{\partial t^2}(x, t) + (R C + G L) \frac{\partial u}{\partial t}(x, t) + G R u(x, t) \]
Enfin, si on se place dans le cas où la ligne est sans pertes, ie R = G = 0, on retrouve une équation d'onde de d'Alembert :
\[ \boxed{\frac{\partial^2 u}{\partial x^2}(x, t) = \frac{1}{c^2} \frac{\partial^2 u}{\partial t^2}(x, t)} \quad \text{avec } c = \frac{1}{\sqrt{L C}} \]
La ligne sera considérée sans pertes dans le reste du document. La solution de l'équation d'onde est de la forme : \(u(x,t)=U_{+}e^{j\omega t}e^{-j\beta x}+U_{-}e^{j\omega t}e^{j\beta x}\), avec :
\[\beta=\frac{2\pi}{\lambda}=\frac{\omega}{v_{\varphi}} \quad \text{et la vitesse de phase } v_{\varphi}=\frac{c}{\sqrt{\varepsilon_{r}}}\]
L'impédance caractéristique est l’impédance de charge pour laquelle l’impédance d’entrée est égale à l’impédance de charge. L'impédance caractéristique dans notre cas s'exprime :
\[ Z_{C} = \frac{1}{\pi} \sqrt{\frac{\mu_0}{\epsilon_0\,\epsilon_r}} \,\mathrm{acosh}\!\biggl(\frac{r_d}{r_a}\biggr). \]
On peut approximer la fonction \(\mathrm{acosh}\) pour l'implémentation en VHDL tel que
\[ Z_{C} = \frac{1}{\pi} \sqrt{\frac{\mu_0}{\epsilon_0 \,\epsilon_r}} \,\log\!\biggl( \frac{r_d}{r_a} + \sqrt{ \biggl(\frac{r_d}{r_a}\biggr)^{2} - 1 } \biggr). \]avec \(r_{d}\) le rayon entre les centres des deux câbles et \(r_{a}\) le rayon d'un câble.
C'est cette expression de l'impédance caractéristique qui sera implémenté dans le modèle de la ligne sur Partquest. On peut maintenant donner le temps de propagation du signal sur la ligne, temps de retard : \(t_{d}=\frac{l}{v_{\varphi}}\). La valeur de \(t_{d}\) permettra de choisir une largeur d'impulsion bien inférieure au temps de retard de la ligne.
3.1.2 - Étude en réflectométrie temporelle
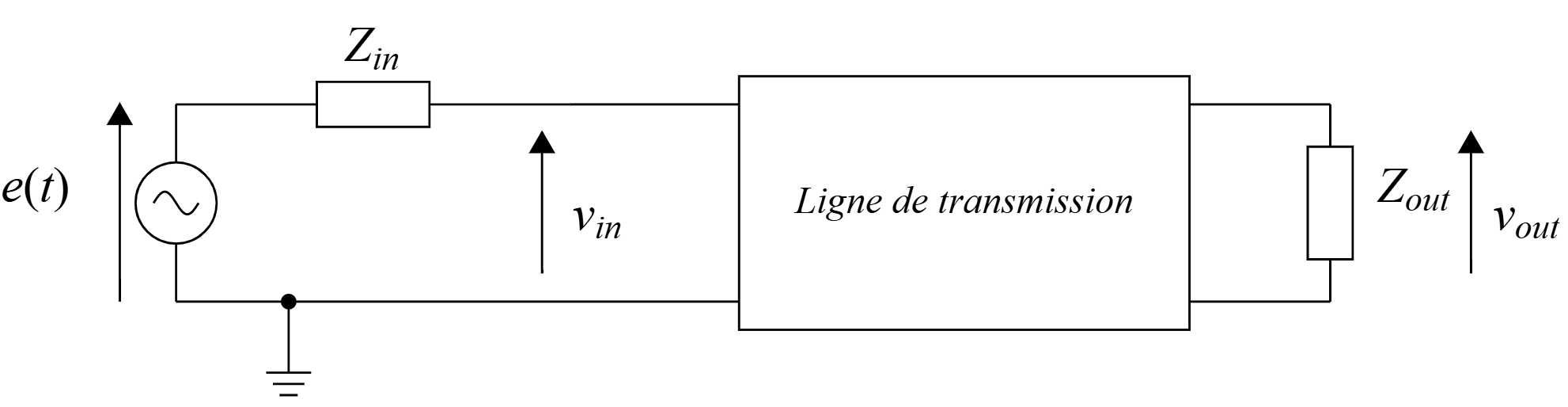
Sachant que le rayon intérieur est de 0.05 m et celui extérieur de 0.5 m, on a une impédance caractéristique \(Z_{C}=119,64 \text{ } \Omega\)
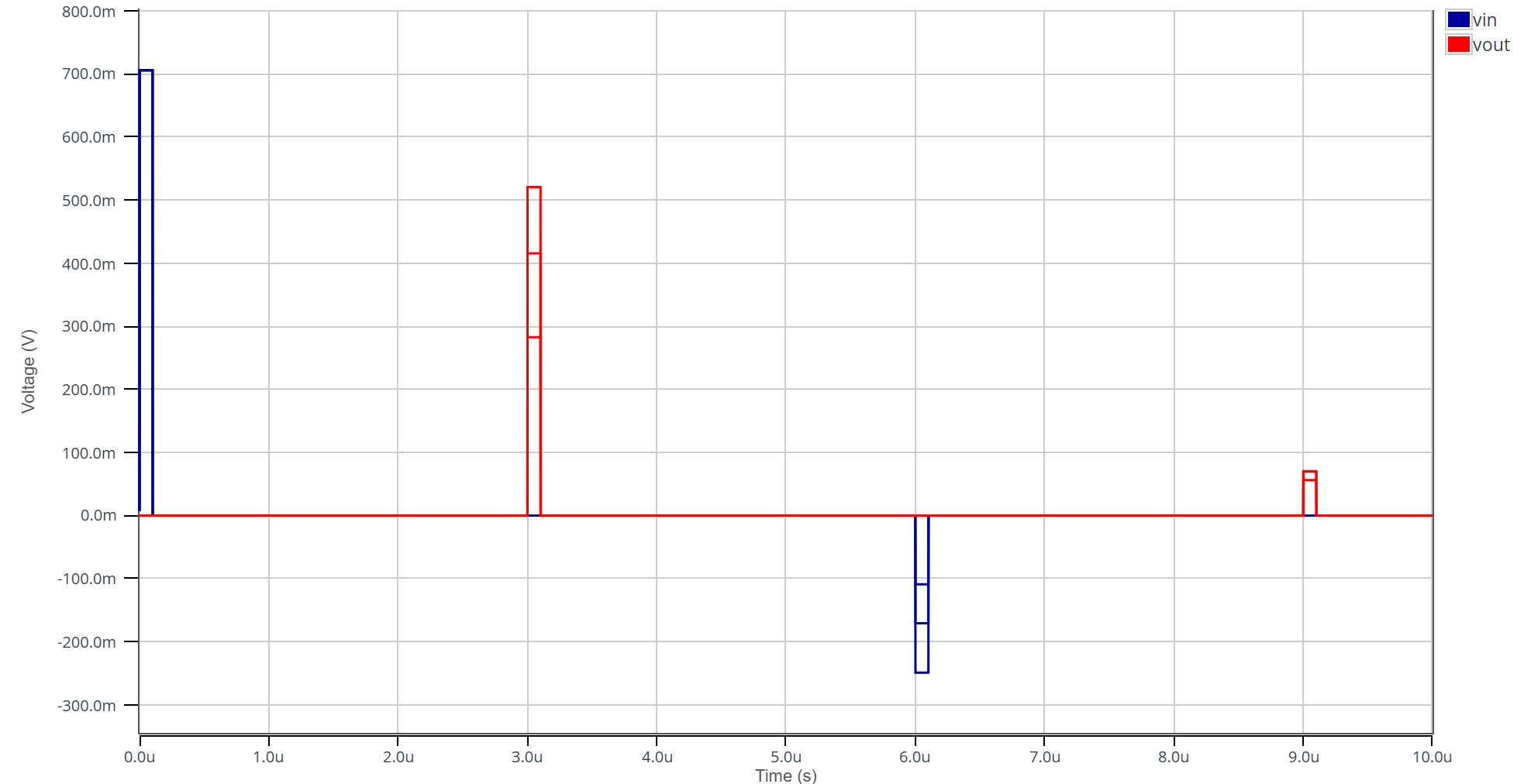
On remarque que, plus la valeur de l'impédance de charge se rapproche de l'impédance caractéristique, plus l'amplitude de l'onde réfléchie diminue. On mesure un temps de propagation de \(3.0 \) \(\mu s\).
3.1.3 - Étude fréquentielle
On fixe l'impédance de charge à \(Z_{L} =\) \(100 \Omega\) pour que la ligne soit désadaptée. Et la longueur de la ligne est fixée à 1m.
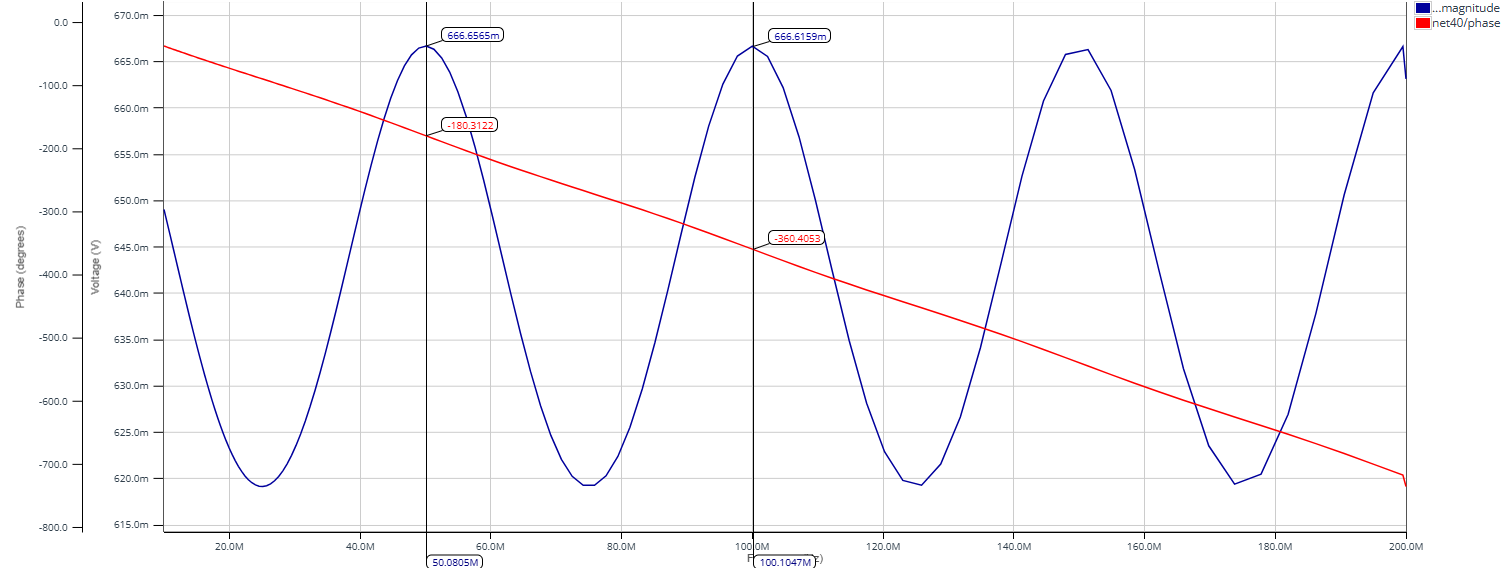
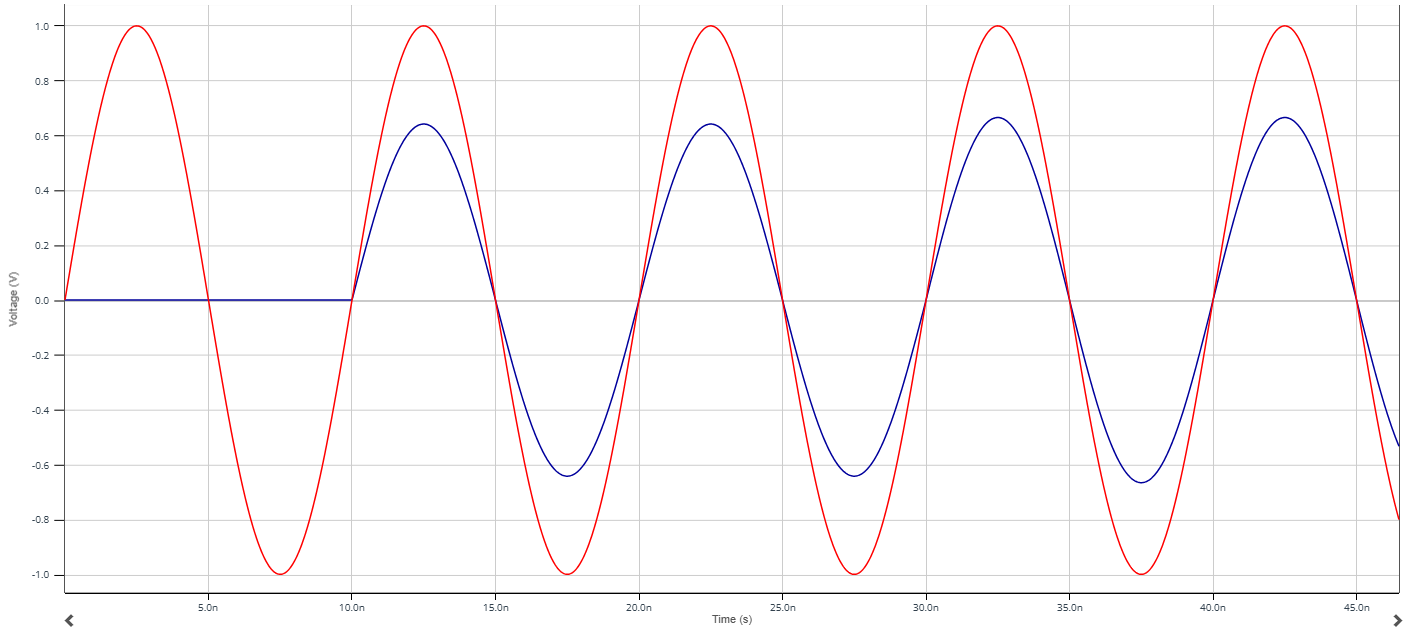
La période fréquentielle est de 50 MHz. Prenons un des maximums, par exemple 100 MHz. On trace alors la réponse temporelle pour cette fréquence. On remarque que les maximums correspondent à une valeur de phase nulle modulo pi. On est alors dans le cas d'interférences constructives, ainsi la longueur de la ligne s'exprime comme :
\[L=n\frac{\lambda}{2},\text{ }\text{ }\text{ }n\in \mathbb{N^{*}}\]
Sachant que \(\lambda=\frac{v}{f}\) et \(v=\frac{c}{\epsilon_{r}}\), on en déduit \[L=\frac{c}{2\sqrt{\epsilon_{r}}\Delta f}\] avec \(\Delta f\) la période fréquentielle (ici 50 MHz). Ainsi \[L=\frac{3\cdot10^8}{2\sqrt{9}\cdot 50\cdot10^6}=1\text{m}\] Ce résultat correspond effectivement à la valeur de ligne fixée dans la simulation.
3.2 - Pont de Wheatstone
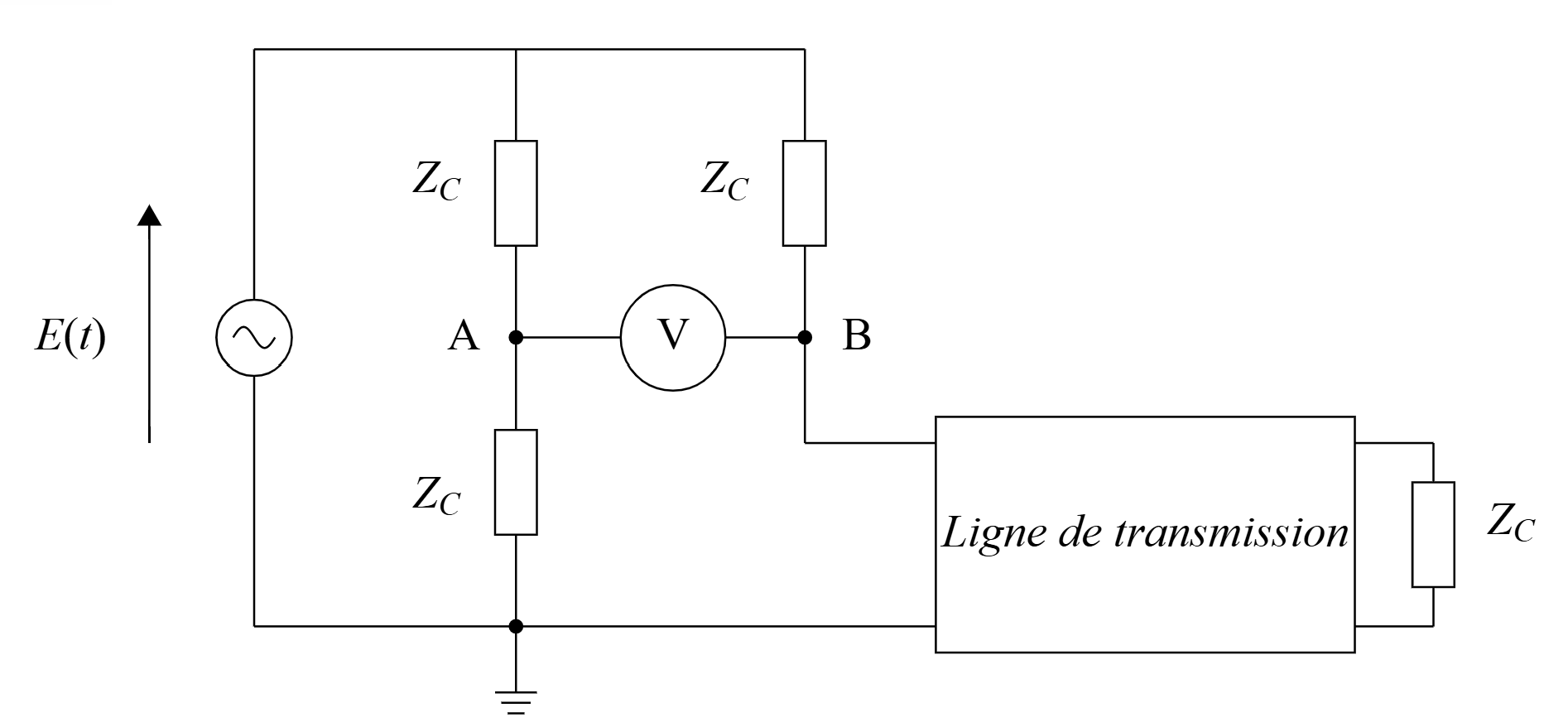
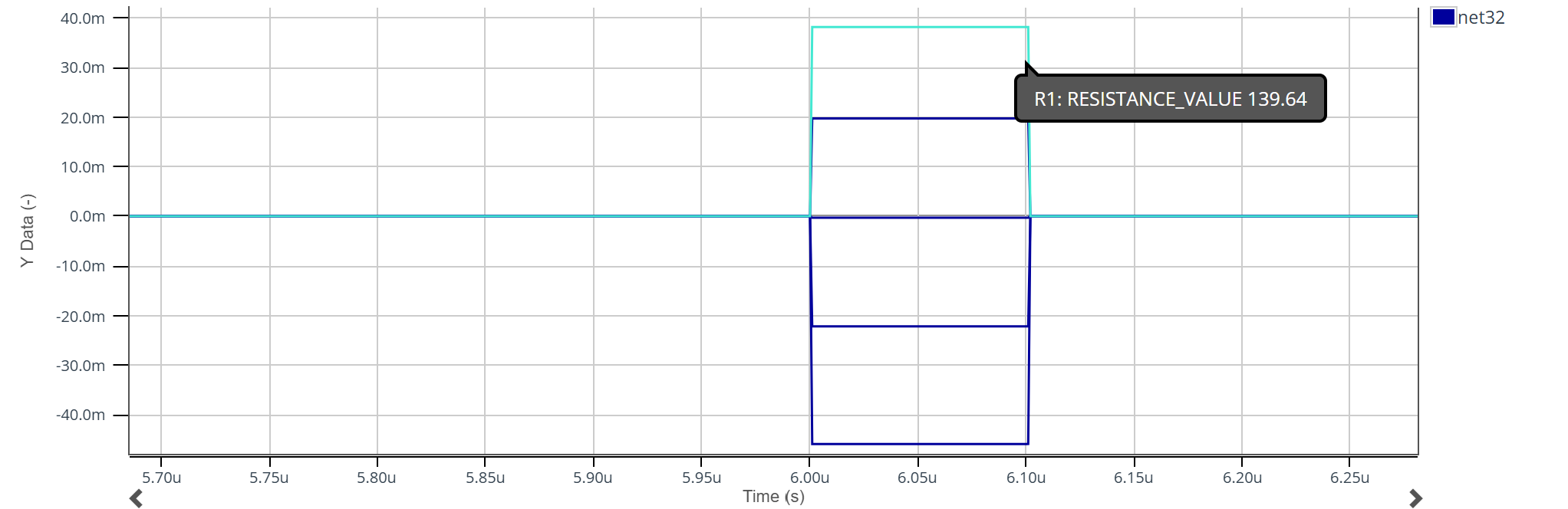
On constate que pour \(Z_{L} = 119,64 \Omega\), la tension en sortie du pont de Wheatstone est nulle. Pour \(Z_{L} > 119,64 \Omega\), la tension de sortie est positive et augmente avec la valeur de \(Z_{L}\). Pour \(Z_{L} < 119,64 \Omega\), la tension de sortie est négative et diminue avec la valeur de \(Z_{L}\).
On en déduit que la tension de sortie du pont de Wheatstone est une fonction affine de \(Z_{L} \) avec \(V(Z_{L}=119,64 \Omega) = 0 V\), où V est la tension en sortie du pont de Wheatstone.
Ainsi, la tension différentielle permet de retranscrire le coefficient de réflexion. Sachant que le potentiel au point \( B \), \( V_B \), dépend de ce coefficient de réflexion, la mesure de la différence de potentiel entre les points \( A \) et \( B \) rend compte des variations de l’humidité.
D’une part : \[ V_A = \frac{E(t)}{2}, \]
D’autre part : \[ V_B = \frac{Z_{\text{in}}}{Z_{\text{in}} + Z_c} E(t). \]
Donc : \[ V_B - V_A = \left( \frac{Z_{\text{in}}}{Z_{\text{in}} + Z_c} - \frac{1}{2} \right) E(t) = \frac{Z_{\text{in}} - Z_c}{2(Z_{\text{in}} + Z_c)} E(t). \]
On obtient la tension de sortie du pont de Wheatstone : \[ V_B - V_A = \Gamma_{\text{in}} \frac{E(t)}{2} \tag{10} \] On remarque que la ligne est désadaptée (\( \Gamma_{\text{in}} \neq 0 \)) si et seulement si la tension observée \( V_B - V_A \) est non nulle.
4 - Modélisation des défauts et classification par réflectométrie temporelle
4.1 - Humidité locale
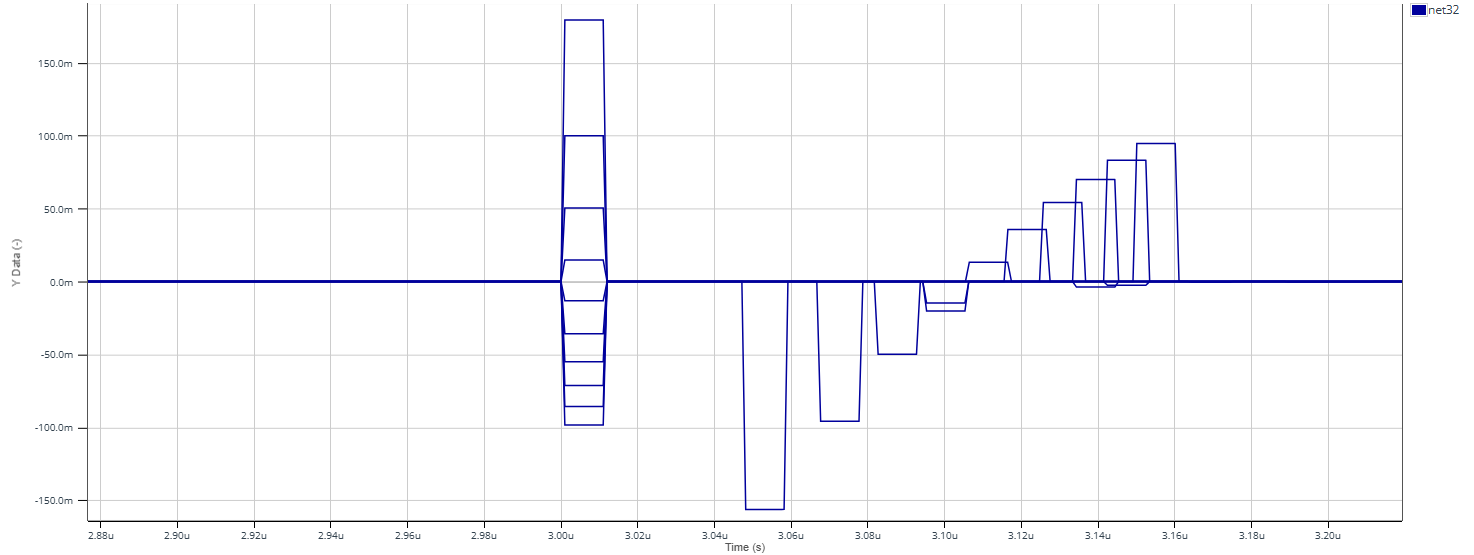
On observe que :
Si \(\epsilon_{r}\) > 9, alors 2 impulsions sont observées l'une après l'autre, la première négative puis la seconde positive.
Si \(\epsilon_{r}\) < 9, alors 2 impulsions sont observées l'une après l'autre, la première positive puis la seconde négative.
Si \(\epsilon_{r}\) = 9, on observe aucune impulsion.
L'amplitude de l'impulsion donne l'information sur la valeur de \(\epsilon_{r}\).
4.2 - Fissure
Pour modéliser une fissure, on place une résistance \(R_{p}\) en parallèle dont on fait varier la valeur entre 200 \(\Omega\) et 500 \(\Omega\).
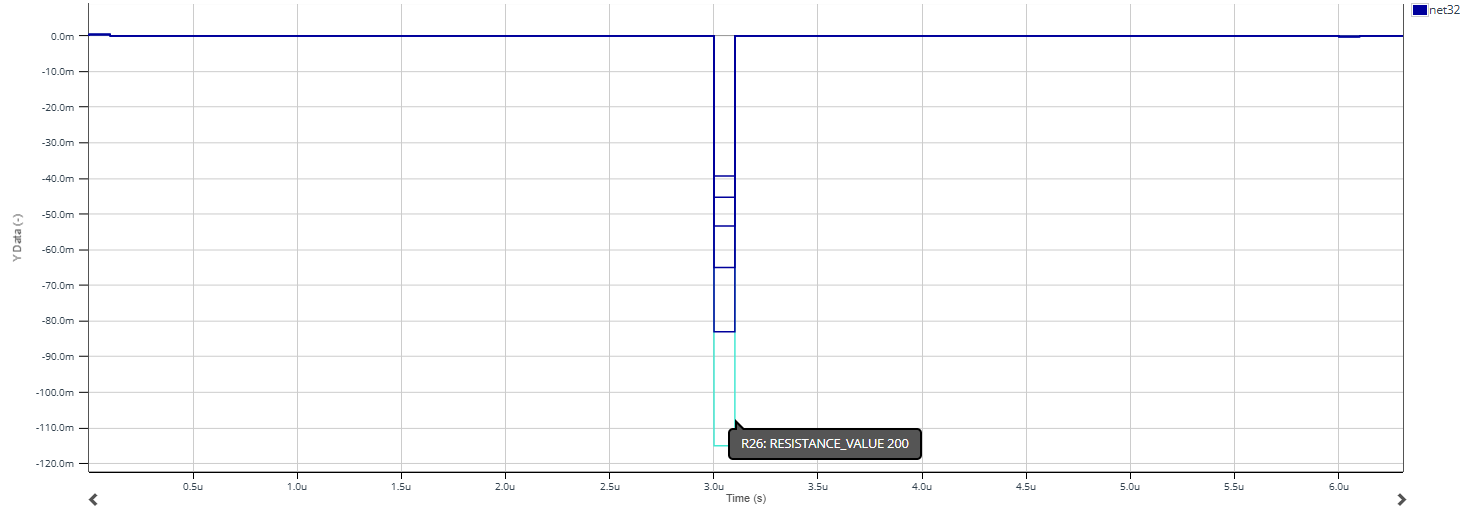
On observe alors plusieurs valeurs d'impulsions réfléchies, dont l'amplitude est fonction de la valeur de \(R_{p}\). En effet, l'amplitude de l'impulsion diminue avec l'augmentation de \(R_{p}\). De plus, les valeurs mesurées sont négatives.
4.3 - Corrosion du câble
On souhaite maintenant la corrosion du câble, on place donc une résistance \(R_{s}\) en série dont on fait varier la valeur entre 1 \(\Omega\) et 10 \(\Omega\).
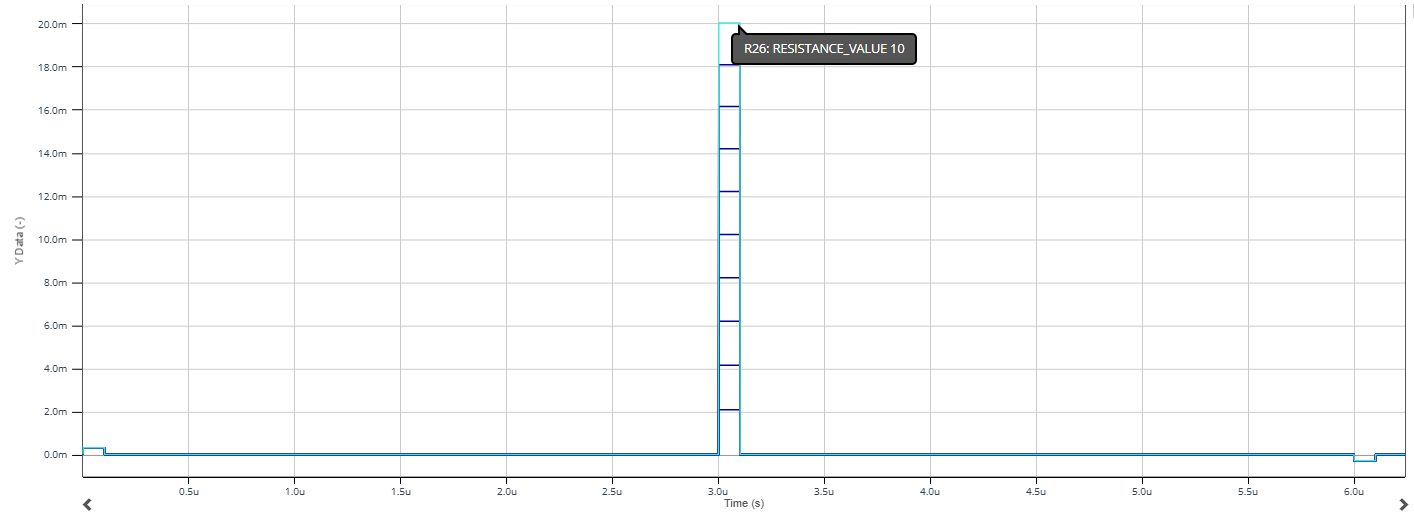
On observe plusieurs valeurs d'impulsions réfléchies, dont l'amplitude est fonction de la valeur de \(R_{s}\). En effet, l'amplitude de l'impulsion augmente avec la valeur de \(R_{s}\). On constate cette fois que les valeurs mesurées sont positives.
5 - Conditionneur
Afin de tester le circuit dans la suite du document on effectue un parameter sweep de \(\epsilon_{r}\) de 9 à 20 par pas de 2.
5.1 - Soustracteur
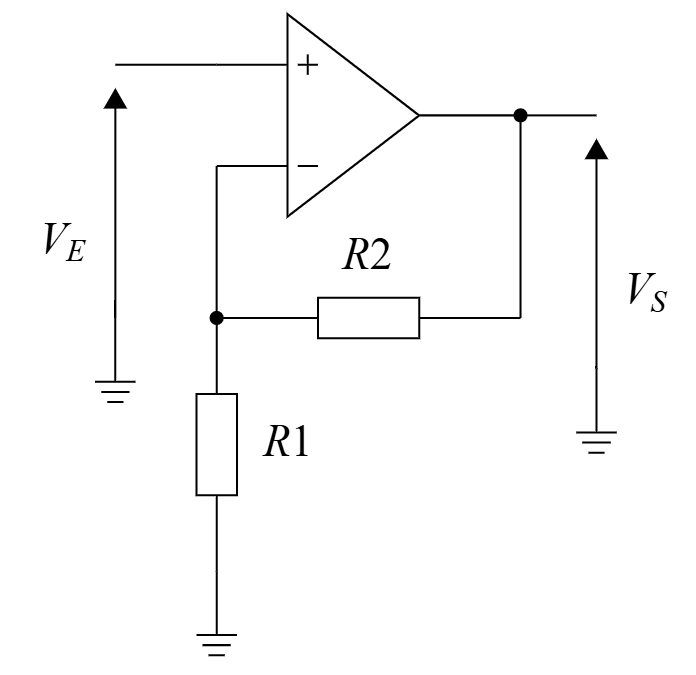
On cherche maintenant à extraire la tension en sortie du pont de Wheatstone. On utilise dans un premier temps un montage soustracteur pour extraire la différence de potentiels.
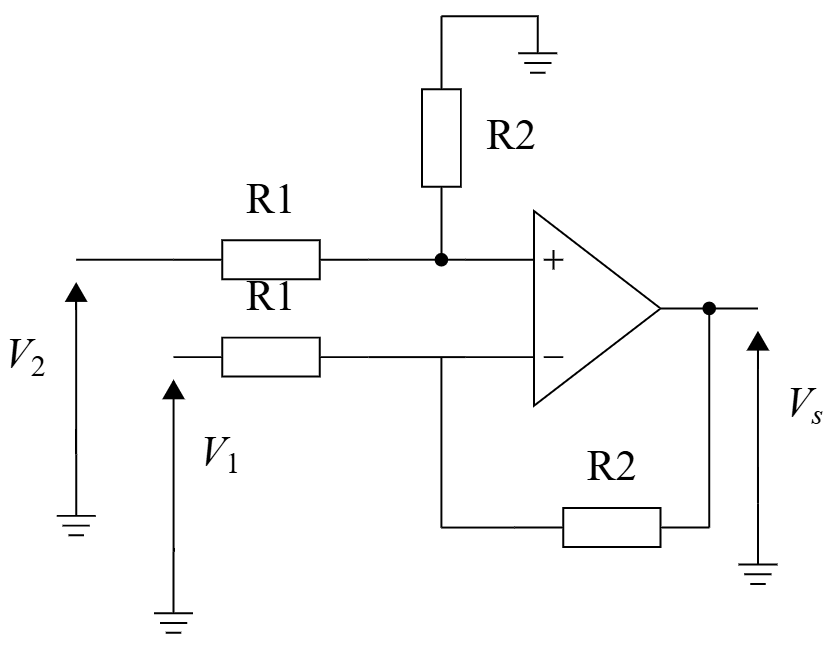
La tension de sortie du montage soustracteur s'exprime comme : \[V_{S}=\frac{R_{2}}{R_{1}}(V_{2}-V_{1})\] On choisit \(R_{1}=50\Omega\) et \(R_{2}=5000\Omega\). De cette façon le gain en sortie du soustracteur est de 100.
5.2 - Détecteur de crêtes
On souhaite maintenant récupérer l'amplitude du signal en sortie du soustracteur puisque cette dernière est directement fonction de la valeur de \(\epsilon_{r}\). On utilise pour ce faire un détecteur de crêtes composé d'une diode suivie d'une résistance et d'un condensateur en parallèles.
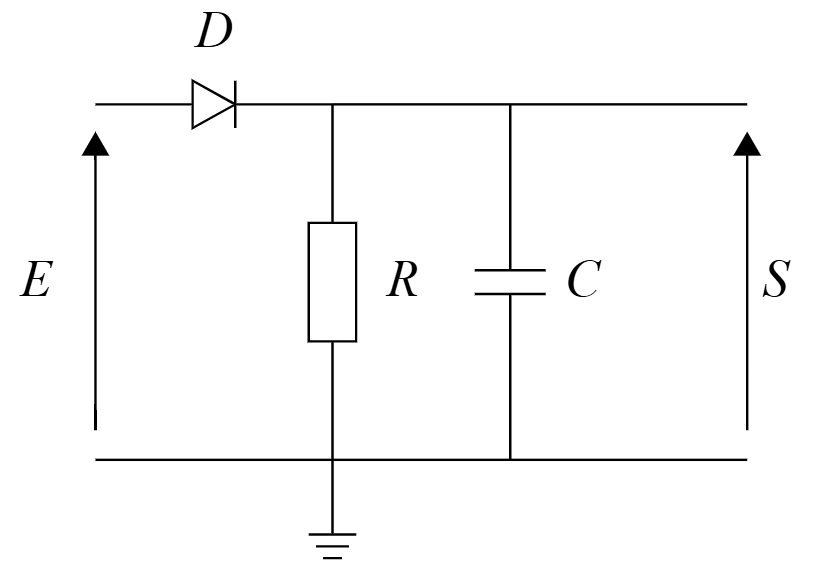
Le choix des valeurs de R et C sont primordiales, car c'est elle qui vont permettre au montage de fournir la tension avec le minimum d'ondulation en tension possible.
Ainsi, on doit choisir R et C de telle façon que le temps caractéristique de décharge du condensateur soit très grand devant la période du signal : \(RC=\tau>>T\) avec T la période du signal en entrée.
En même temps, \(\tau\) ne doit pas être trop grand pour permettre au signal en sortie du détecteur de crêtes d'atteindre le plus vite possible sa valeur finale et éviter que la réponse du circuit final soit trop "lente".
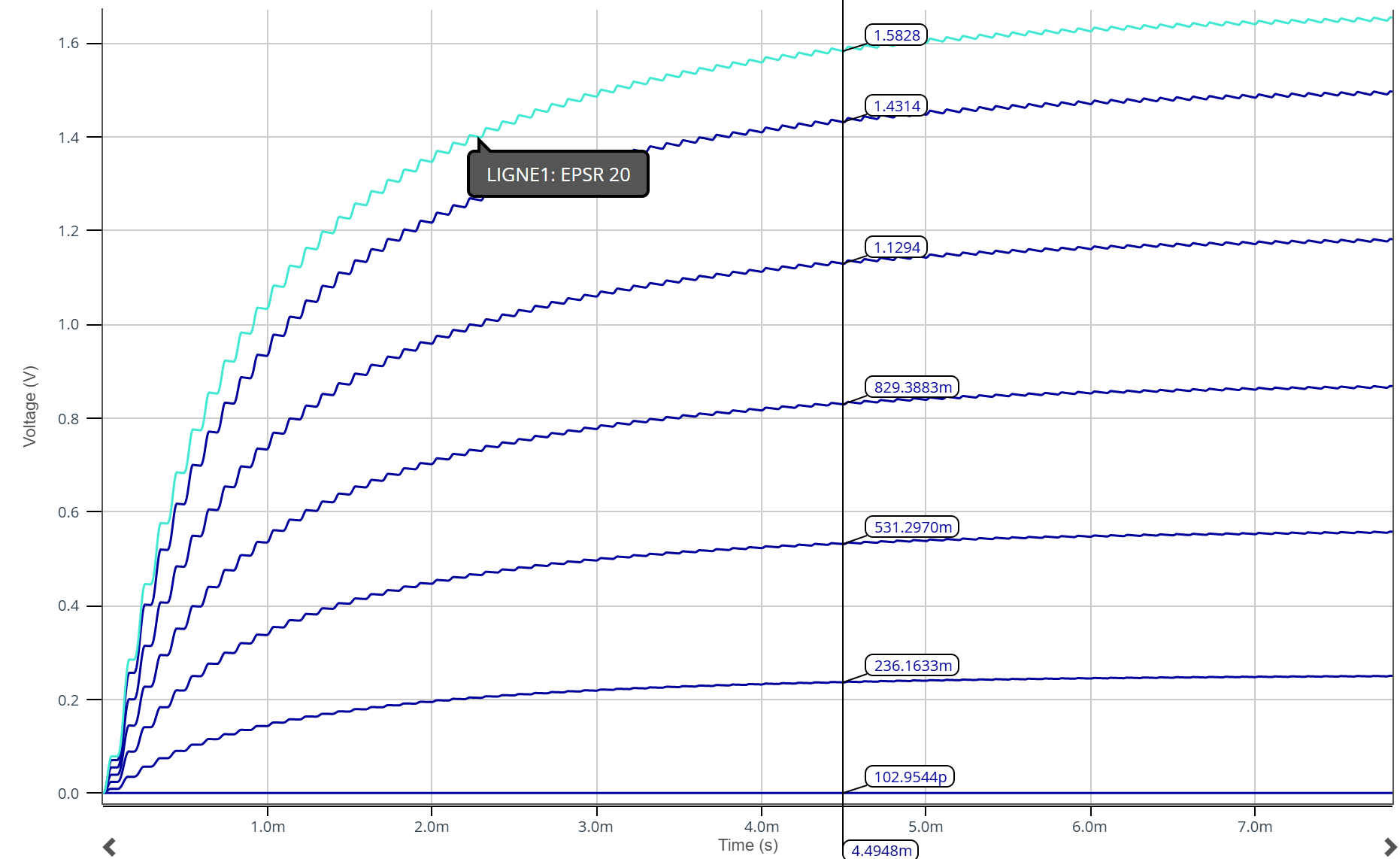
On mesure un temps de réponse à 5% du circuit de 4,5 ms.
5.3 - Amplification du signal
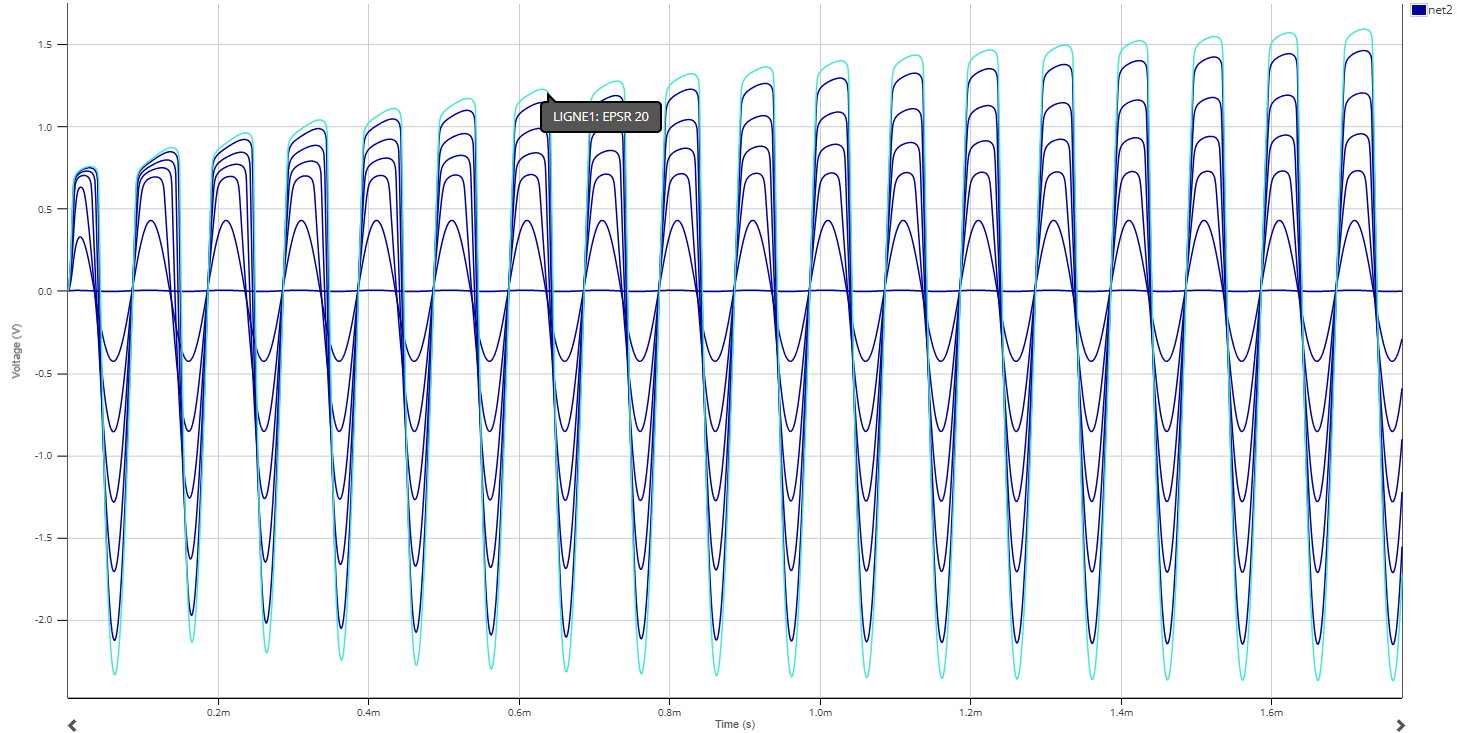
En analysant les résultats des simulations, on s’aperçoit que la tension en sortie du détecteur de crêtes est très faible. Or, on voudrait que pour \(\epsilon_{r}=20\) on ait une tension de sortie pleine échelle de 3,3 V.
On mesure une tension de sortie de 1.28 V en sortie du détecteur de crêtes. Donc pour avoir 3.3 V on doit avoir un amplificateur avec un gain de \(\frac{3,3}{1,28}=2,26\). Or, la tension en sortie de l'amplificateur non-inverseur s’exprime : \[V_{S}=(1+\frac{R_{2}}{R_{1}})V_{E}\] En prenant \(R_{1}=1k\Omega\) et \(R_{2}=1,6k\Omega\) on a un gain de 2,27.
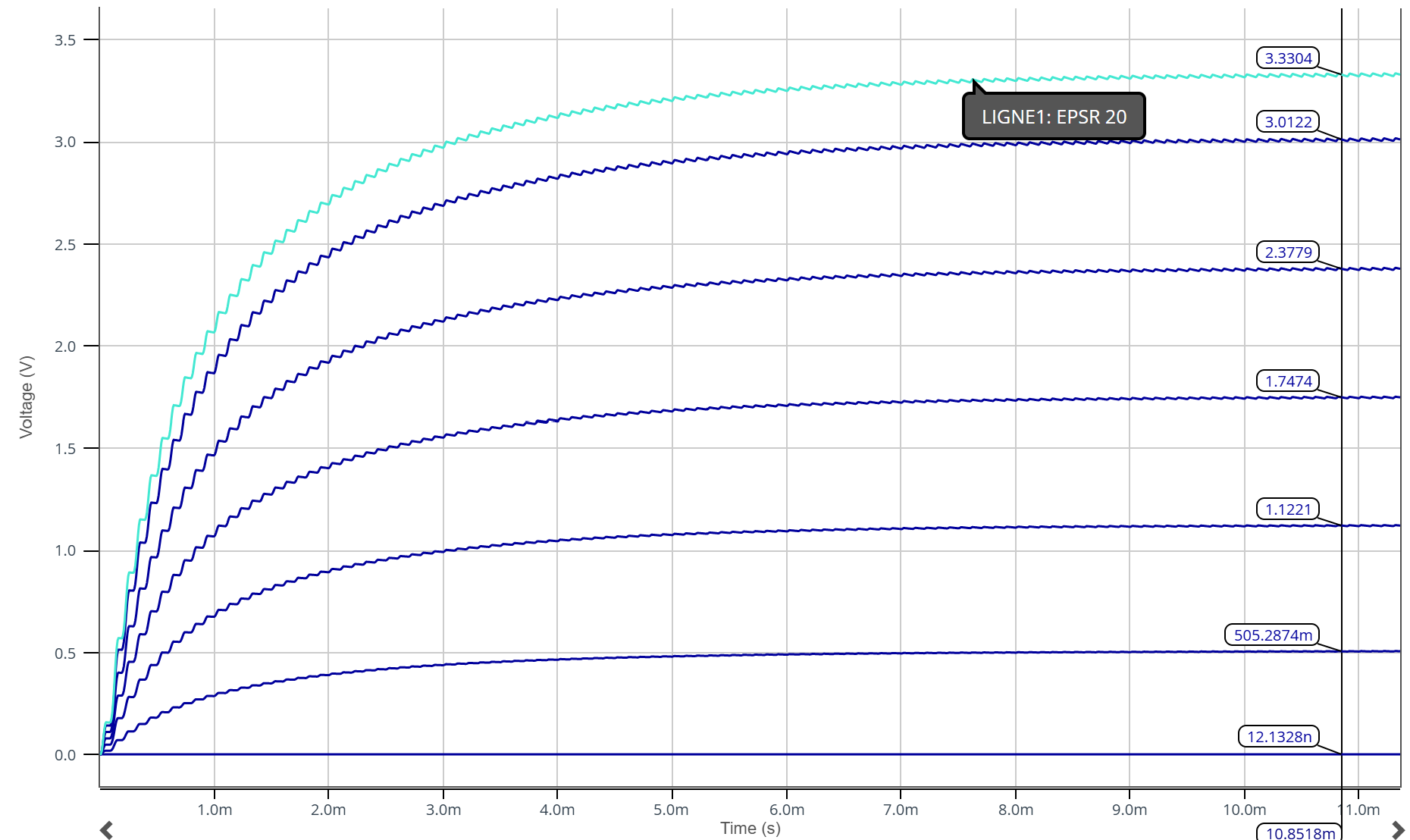
On mesure donc bien 3,3 V en sortie de l'amplificateur pour \(\epsilon_{r}\) = 20.
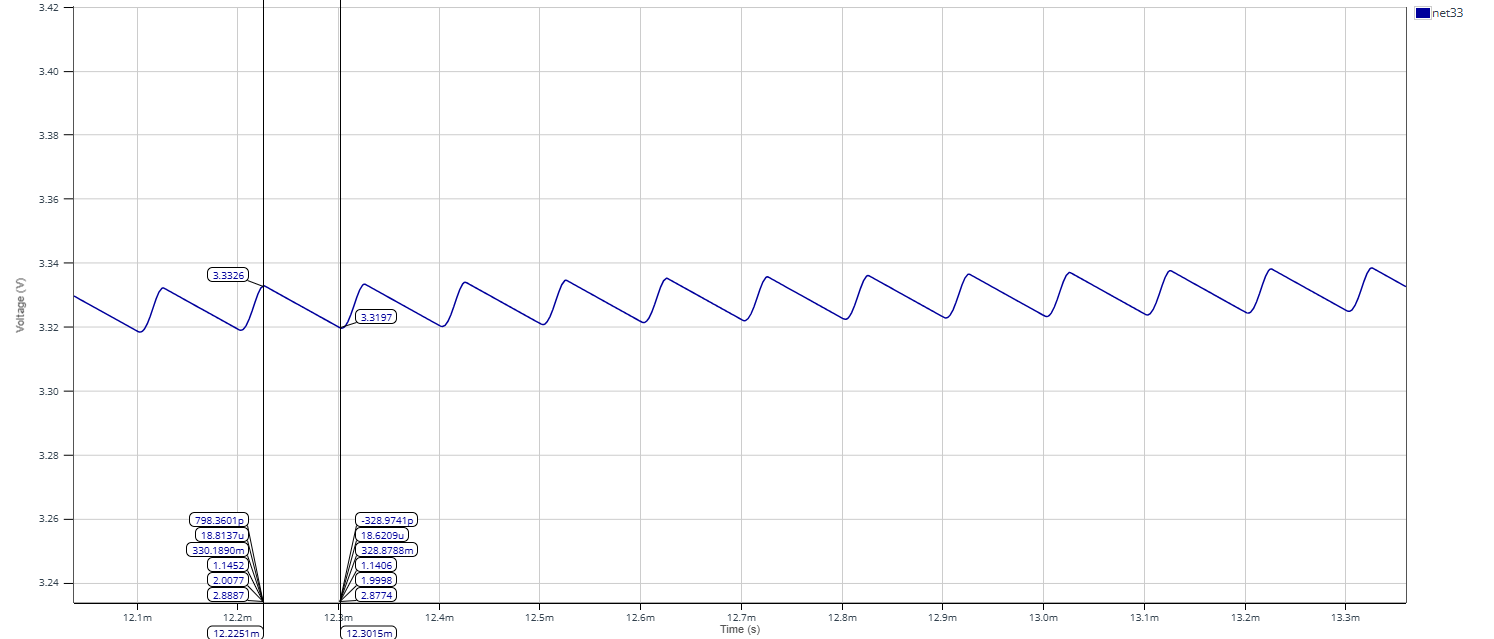
On mesure une ondulation en tension de 10 mV au maximum pour $\epsilon_{r}$ = 20 ce qui est relativement peu et permet de ne pas perturber significativement le comportement d'un microcontrôleur que l'on pourrait placer en sortie du circuit par exemple.
5 - Vérifications et synthèse
Ci-dessous l'architecture finale du circuit sur Partquest. On y retrouve les 5 grands sous-systèmes à savoir le Pont de Wheatstone, la ligne de transmission et le conditionneur composé du soustracteur, du détecteur de crêtes et enfin de l'amplificateur.

On effectue un parameter sweep avec un pas de 1 pour avoir la meilleure précision pour la régression.
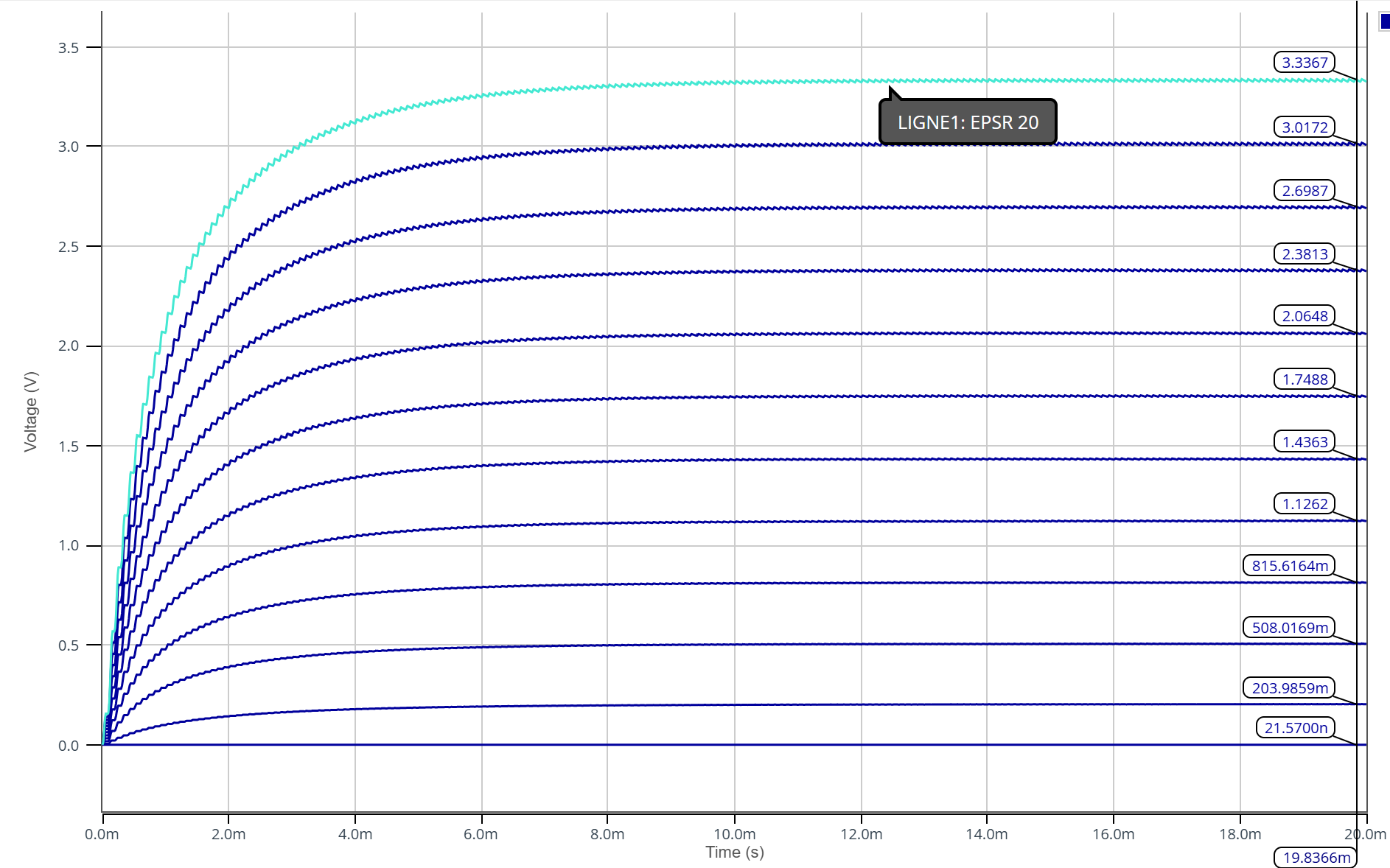
On peut tracer ensuite sur Python la permittivité relative en fonction de la tension et effectuer une régression affine.
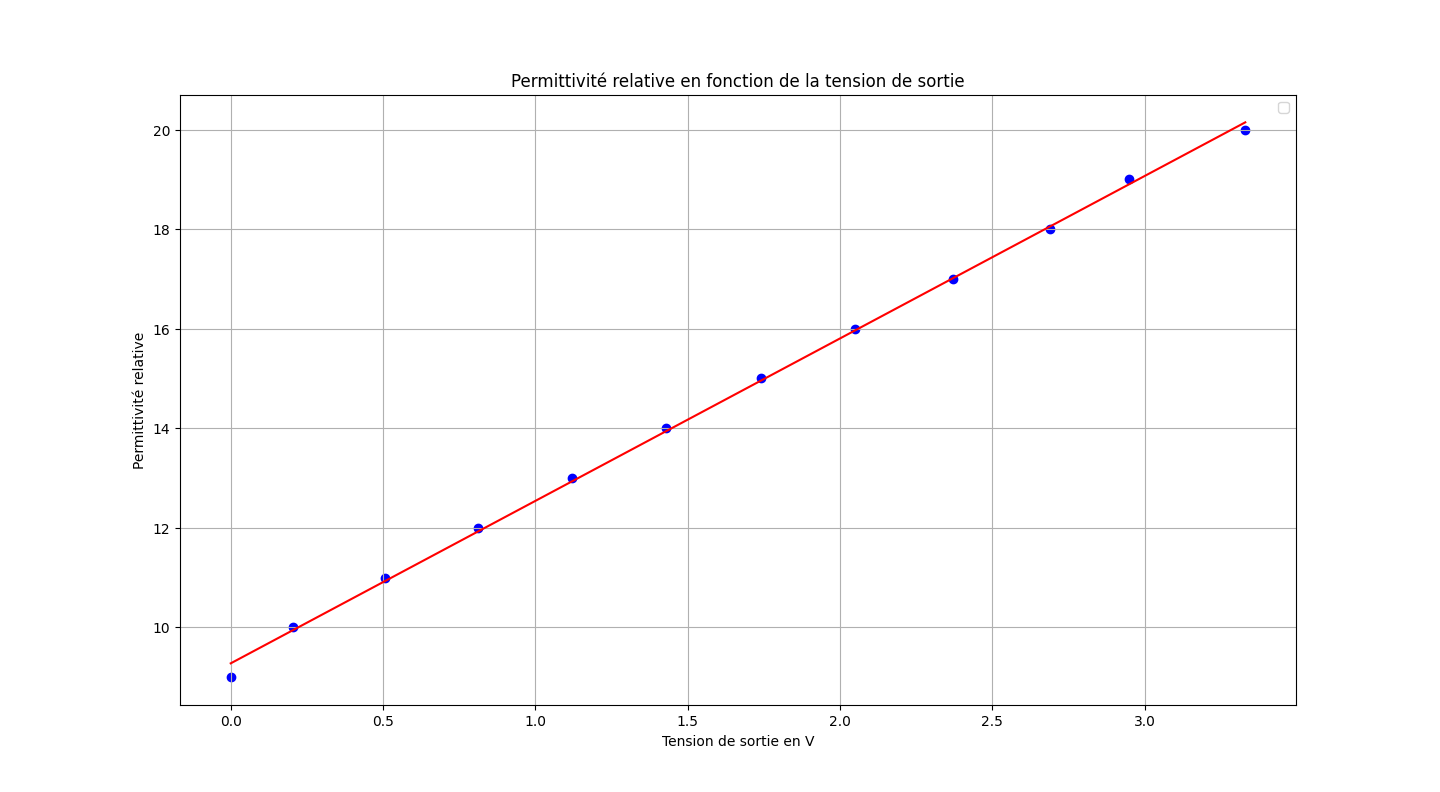
Le coefficient de détermination \(R^2\) est de 0.99 ce qui donne une indication de la validité de la régression. On a alors la loi de comportement entre la tension et \(\epsilon_{r}\) : \[\epsilon_{r}(U)=3,26\cdot U+9,2\]
6 - Conclusion
Ce projet a permis de développer un système de mesure en quasi temps réel de la qualité du béton précontraint. Basé sur une ligne de transmission couplée à un pont de Wheatstone et un système de conditionnement du signal, notre dispositif permet la détection et la caractérisation de l'humidité locale. Les simulations montrent une excellente linéarité de la réponse avec un R² de 0,99 et un temps de réponse de 4,5 ms. Pour améliorer ce système, un microcontrôleur pourrait être intégré afin d'analyser la tension en sortie et d'optimiser la gestion des données pour une analyse plus précise et en temps réel. Bien que ces résultats soient prometteurs, des tests en conditions réelles seront nécessaires pour valider pleinement le concept.