DESIGN OF A CAPACITIVE SENSOR

Design and Fabrication of a Variable Distance Keypad

1 - Introduction

Since its invention in the 1960s, the keypad has revolutionized how we secure spaces and belongings. Initially designed to replace physical keys with access codes, this system quickly gained popularity due to its simplicity and effectiveness. However, with advancing technology, traditional keypads now reveal certain limitations, such as vulnerability to code theft through wear marks on buttons or the potential transmission of diseases via physical touch. Addressing these issues, our proximity-detection keypad with multiple positions offers solutions to these challenges. This authentication device provides a more secure, intuitive, and contactless alternative. Using multiple electrodes and detecting the distance of the user’s finger, our keypad creates more complex combinations, making code theft significantly harder.

1.1 - Problem Statement and Objectives

The evolution of technologies and security needs has highlighted certain limitations of traditional keypads. While widely adopted, these devices are vulnerable to access code theft, often due to wear marks left on buttons. Moreover, repeated handling of buttons by multiple users raises hygiene concerns, facilitating the transmission of bacteria. In response to these challenges, this project aims to design a proximity-detection keypad with multiple positions.

The specific objectives of the project are as follows:

1.2 - Methods and Selected Technical Solutions

To achieve the set objectives, several methods and technical solutions were implemented:

2 - General Overview of the Project

Schema
Complete Circuit Diagram

2.1 - Capacitive Sensors

Capacitive sensors are the central elements of this project. Their operating principle is based on measuring the electrical capacitance between an electrode and the user’s hand. This capacitance varies depending on the distance between them, enabling the detection of proximity and the finger’s position without physical contact.

The goal is to create a variable capacitance capacitor. In the theoretical model of an infinite parallel plate capacitor, the capacitance \(C\) is expressed as follows:

\[ C = \frac{\varepsilon_0 \varepsilon_r S}{d} \]

where: \(\varepsilon_0\) is the permittivity of free space, \(\varepsilon_r\) is the relative permittivity of the material between the plates, \(S\) is the surface area of the plates, and \(d\) is the distance between the plates.

The derivation of this formula is detailed in section 7.2 - Demonstrations.

Although our capacitors are not infinite, this approximation is sufficiently accurate for the intended application.

In our application, while the infinite plate capacitor model is not strictly valid, it effectively illustrates the inverse proportional relationship between capacitance and the distance \(d\) between the electrode and the user’s hand. Capacitance is also directly proportional to the electrode’s surface area.

Practically, we use three electrodes to generate different combinations for the keypad. A simulation in Comsol demonstrates the distribution of electric field lines when a hand is placed above the central electrode. The field lines from adjacent electrodes curve toward the hand, influencing the capacitance measurement of the central electrode.

2.2 - Need for a Signal Conditioner

To utilize the capacitance variations measured by the capacitive sensors, a signal conditioning circuit is essential. This circuit processes and generates reliable signals from the electrodes.

Direct capacitance measurement is challenging. Methods such as using the resonance of an RLC circuit or a Sauty-Wien bridge could be employed. However, these approaches are generally less precise, more complex to calibrate, and more susceptible to ambient noise. Charging a capacitor with a constant current provides the best compromise, offering high precision.

2.3 - Operation of the Signal Conditioner

The method to determine capacitance involves charging the capacitor with a constant current. The capacitance is then deduced from the time required to reach a specific voltage threshold. This approach requires a precise and stable circuit to ensure reliable measurements.

The design of the signal conditioner includes several key components:

2.4 - Multi-Position Keypad System

Initially, each electrode is calibrated to measure a baseline capacitance in the absence of any conductive object nearby. A detection threshold is then defined to identify two distinct proximity zones of the hand relative to each sensor: near and far.

When a hand approaches the electrodes, the microcontroller detects the capacitance variations and evaluates the hand’s distance. A combination of touch points and distances can be recorded as an access code. For instance, an input sequence could be:

"Sensor 2 near + Sensor 1 far then near + Sensor 3 far." The system then validates the code by comparing the user’s input sequence and distances with a pre-registered sequence. If the sensor distances and sequence match, access is granted.

3 - Design of the Capacitive Sensor

First, we will explore the fundamental operating principle of the capacitive sensor. Next, we will examine why a signal conditioner is necessary for processing and generating the electrode signal. Following that, we will detail the design of such a conditioner, and finally, we will conduct tests and measurements on the conditioning circuit.

3.1 - Operating Principle

The goal is to build a variable-capacitance capacitor. In the model of an infinite parallel plate capacitor (without edge effects), capacitance is expressed as: \[ C = \frac{\varepsilon_{0}\varepsilon_{r}S}{d} \] Although this model does not strictly apply here, it provides insight into how capacitance varies with the distance \(d\) between the two plates (in this case, the electrode and the user’s hand): Capacitance is inversely proportional to the inter-plate distance. Additionally, capacitance is directly proportional to the surface area \(S\) of the electrode.

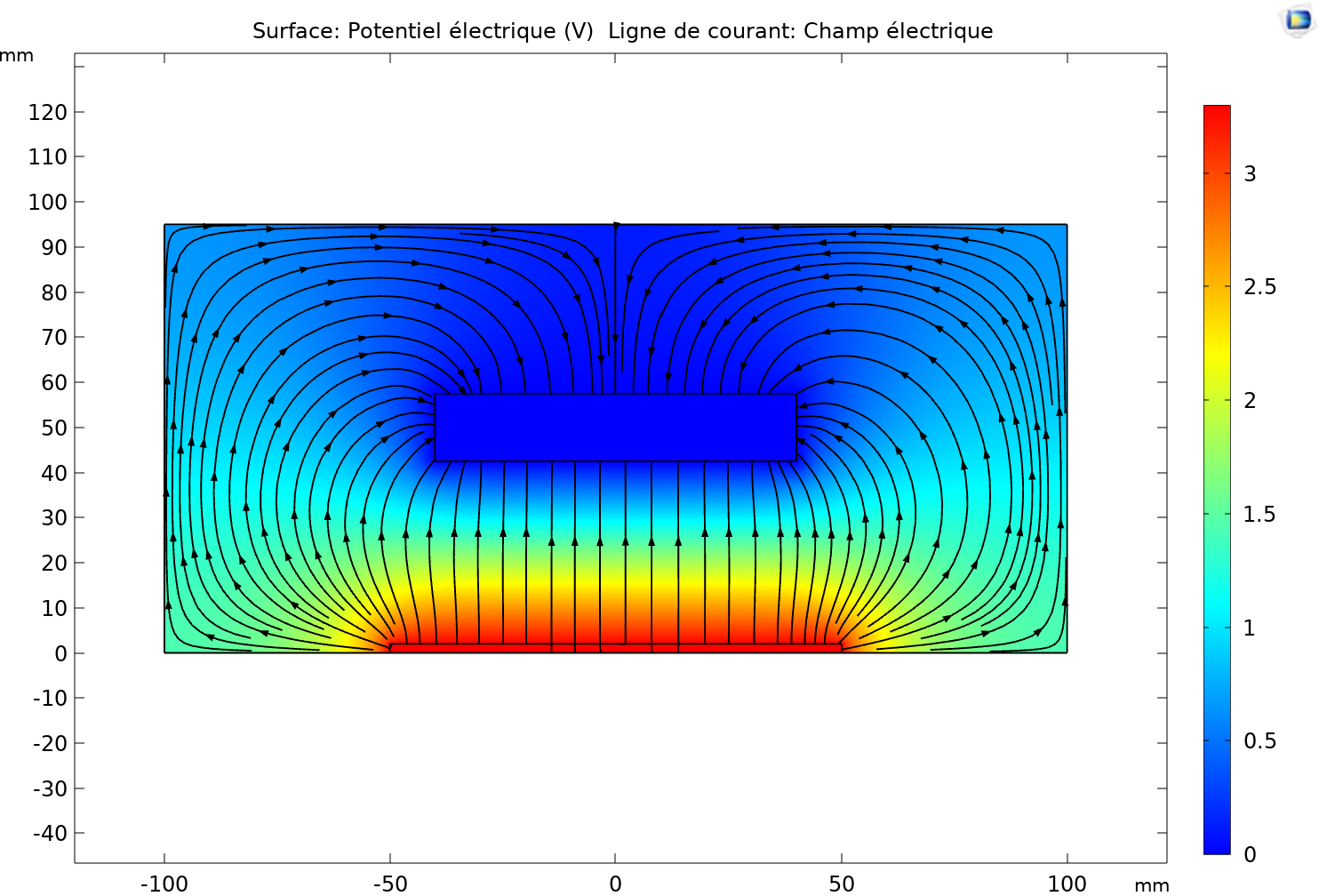
Schema
2D Simulation in Comsol

In practice, three electrodes are used for the keypad combinations. After simulation, when the hand is placed above the central electrode, the following simulation result is obtained:

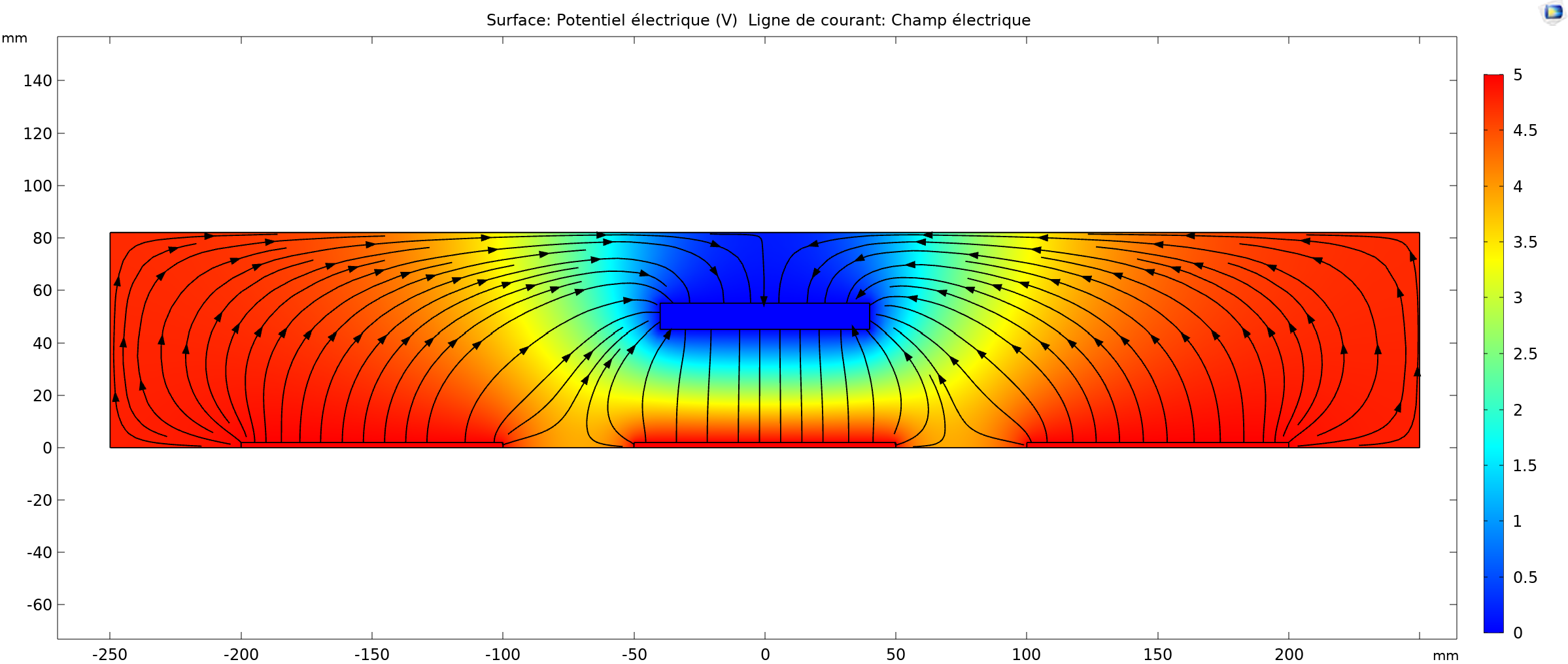
Schema
2D Simulation in Comsol with Three Electrodes

Comparing the two simulations, it can be observed that the field lines from the electrodes on either side of the target electrode bend toward the hand.

We aim to estimate the error caused by the presence of the other electrodes.

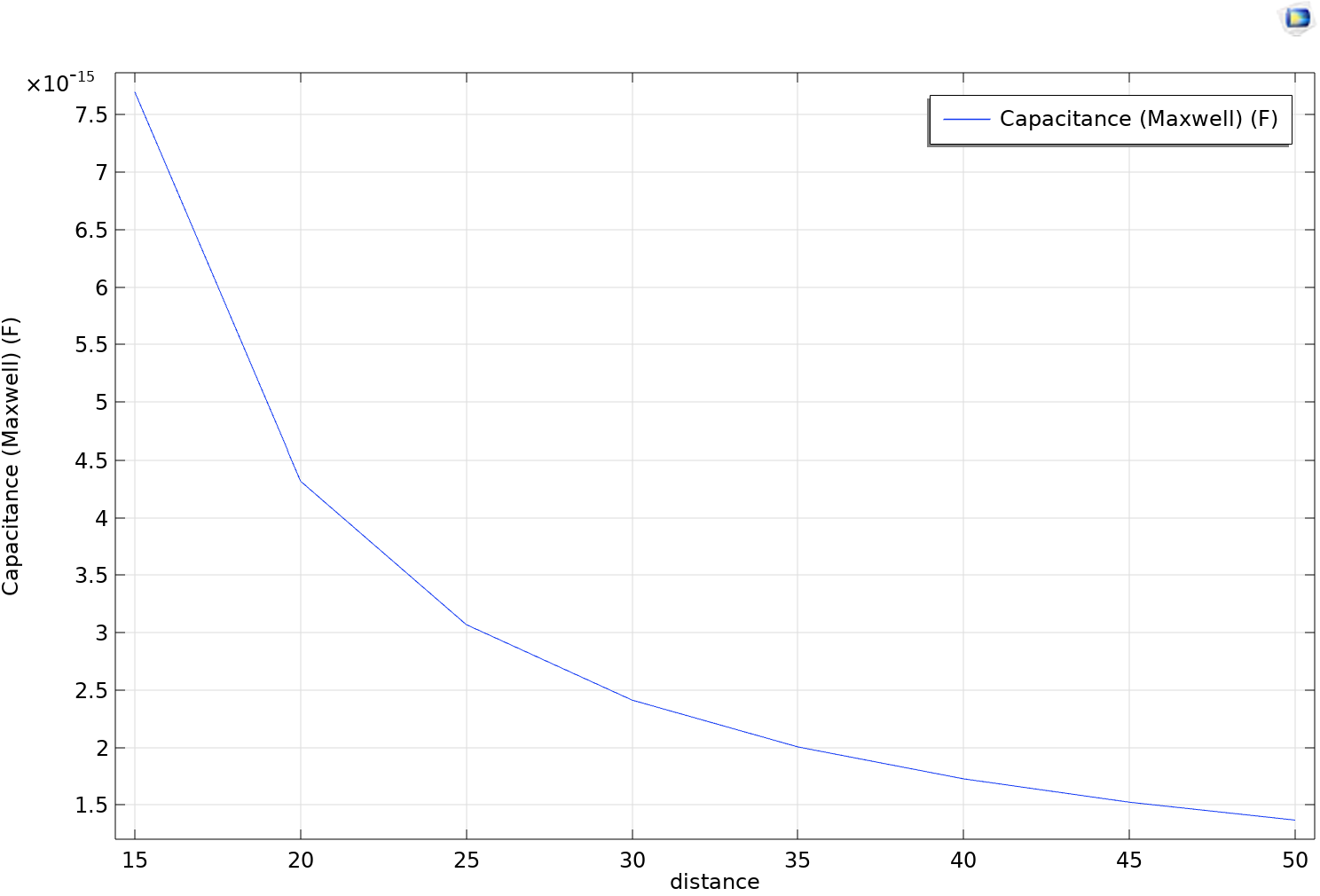
Schema
Capacitance vs. Distance for Three Electrodes (in mm)
Schema
Capacitance vs. Distance for One Electrode (in mm)

The presence of the two other electrodes does not appear to significantly disrupt the system's ability to determine the distance between the hand and the target electrode.

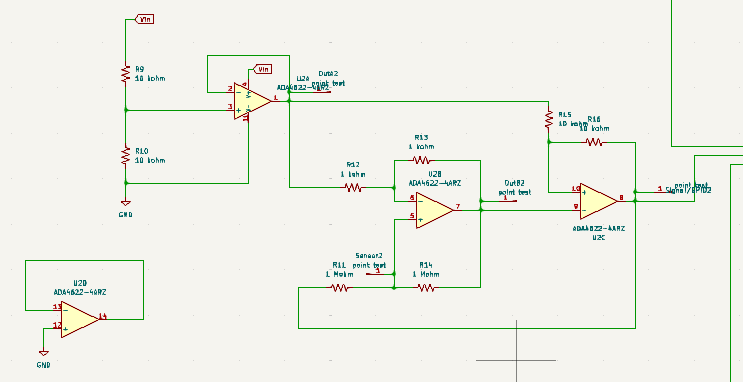
3.2 - Conditioner Design

The design of the conditioner is divided into several distinct parts:

The method for determining the capacitance consists of charging a capacitor (here, the capacitor is formed by the user's hand and the electrode connected to the conditioner circuit) with a constant current. The capacitance can be determined as a function of the charging time.

3.2.1 - Charging a Capacitor with Constant Current
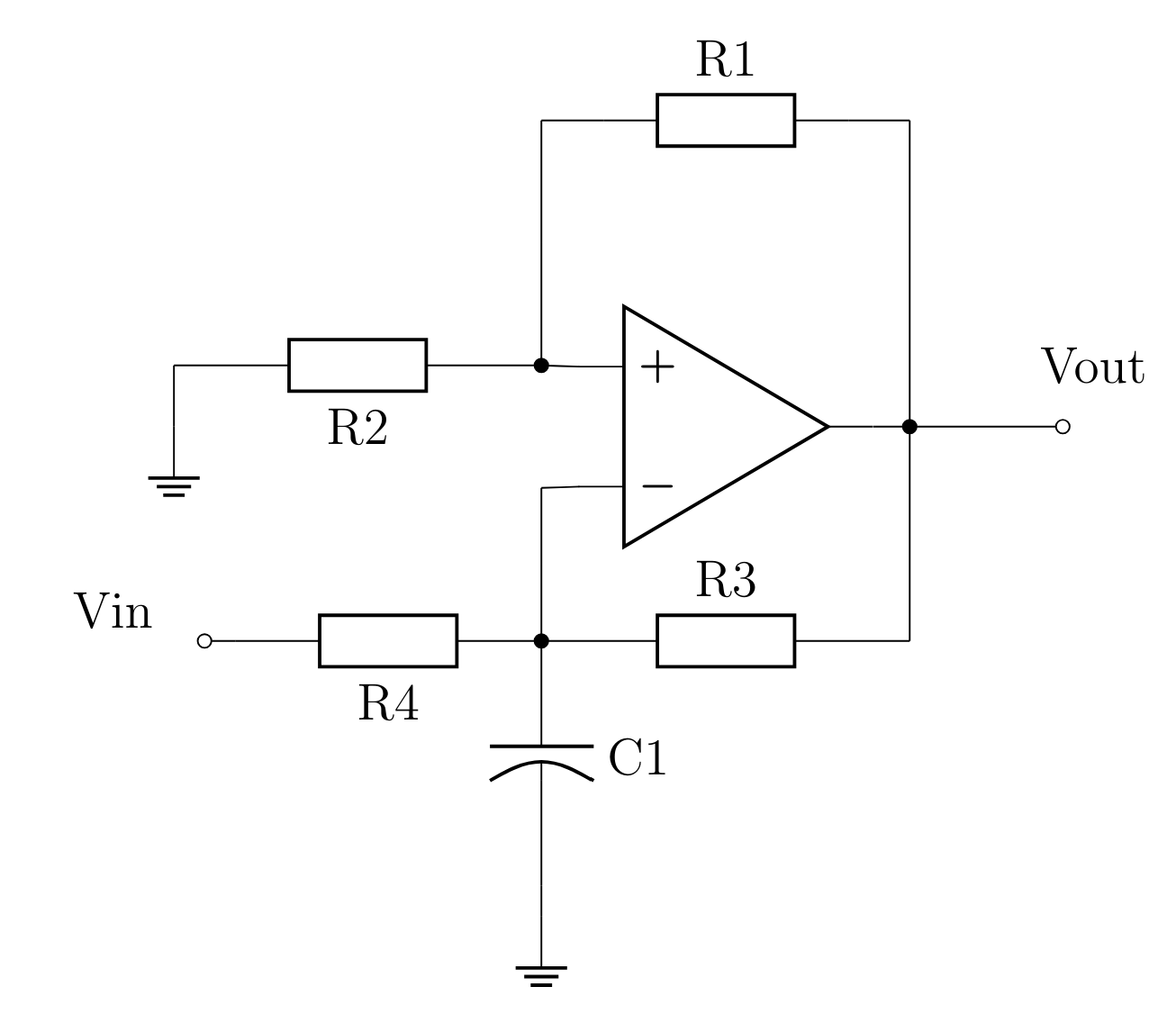
Schema
Constant current charging circuit (the + and - terminals of the op-amp are reversed)

The circuit provides a constant current to the capacitance C1. The charging voltage becomes a linear function, which allows direct correlation of the capacitance value to the circuit's oscillation frequency, which depends on the capacitor's charging time.

The current received by the capacitor is \(i = \frac{Vin}{R_4}\). In PartQuest, we model the circuit for charging the capacitor with a constant current.

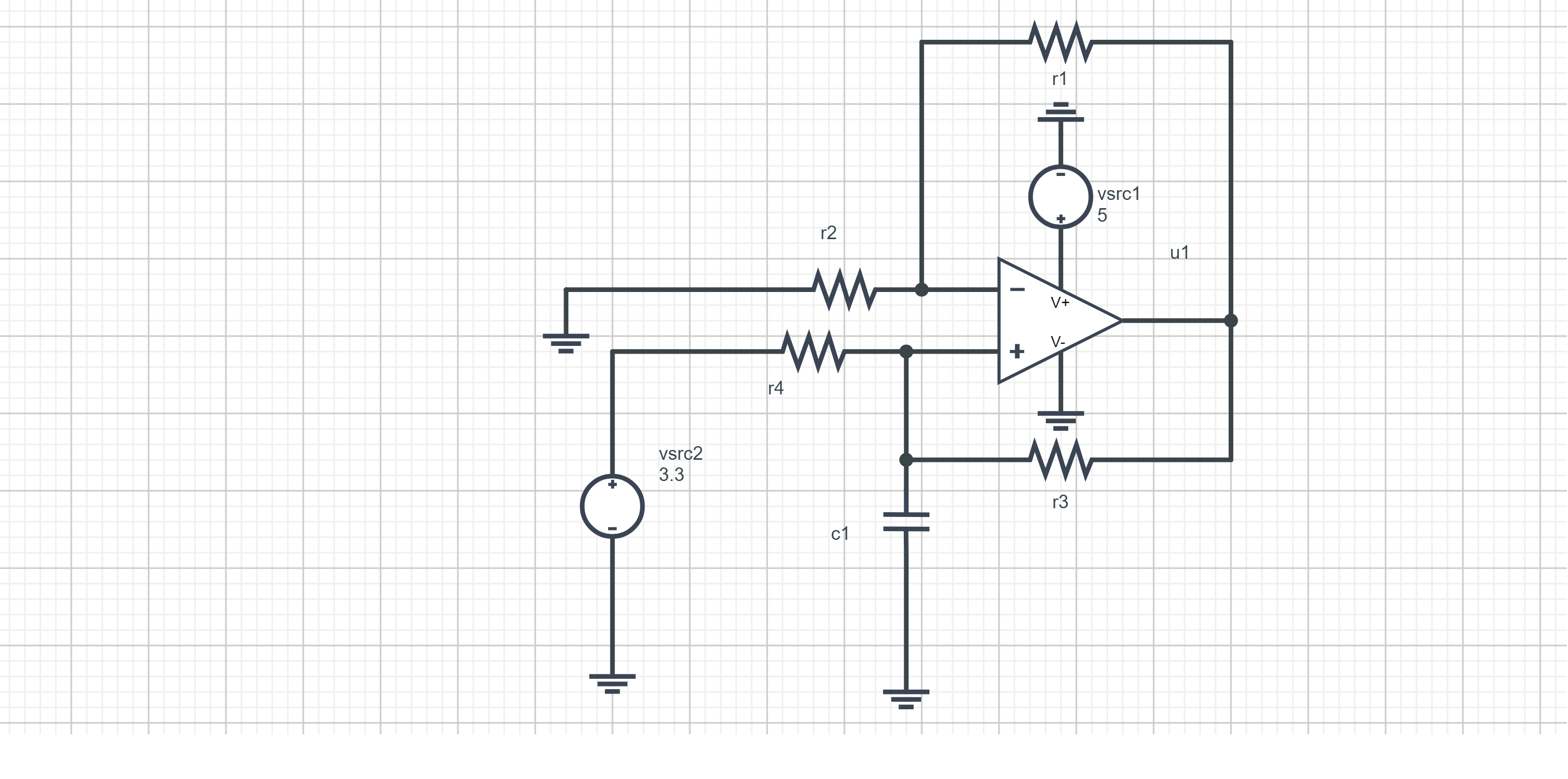
Schema
Constant current charging circuit in PartQuest

We set R1 = R2 = 1 M\(\Omega\). Also, R3 = R4 = nR1 = nR2. Here, we chose n = 4, so R3 = R4 = 4 M\(\Omega\). We take C1 = 10 pF. The op-amp is powered asymmetrically with 0V and 5V. Vin is set to 3.3 V.

This gives the following simulation:

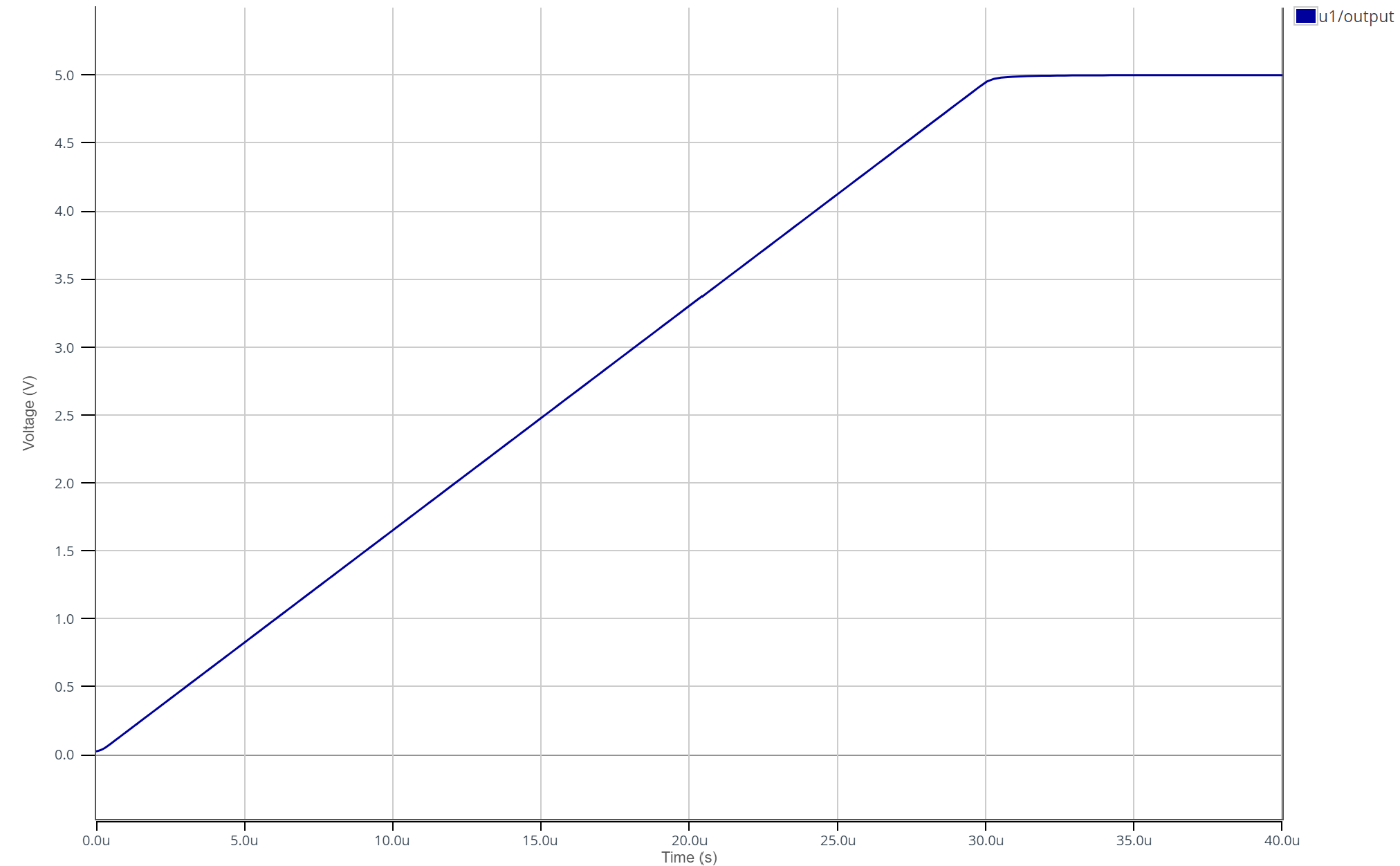
Schema
Capacitor constant current charging in PartQuest

A voltage saturation is observed at 5V, which corresponds to the op-amp's power supply. A linear charging of the capacitor is also observed.

The equation governing the behavior of a capacitor is \(i_C = C\frac{d u_C}{dt}\). We measure a slope \(\frac{d u_C}{dt} = 1.6 \cdot 10^5 \text{ V/s}\). Knowing that the charging current is 8.25e-7 A, we determine the capacitance \(C1= \frac{\frac{du_{C}}{dt}}{i_c} = \frac{1.6 \cdot 10^5}{8.25 \cdot 10^{-7}} = 5.5 \text{ pF}\).

3.2.2 - Hysteresis Comparator

Next, it is necessary to design the hysteresis comparator in order to detect the trigger threshold for closed-loop operation.

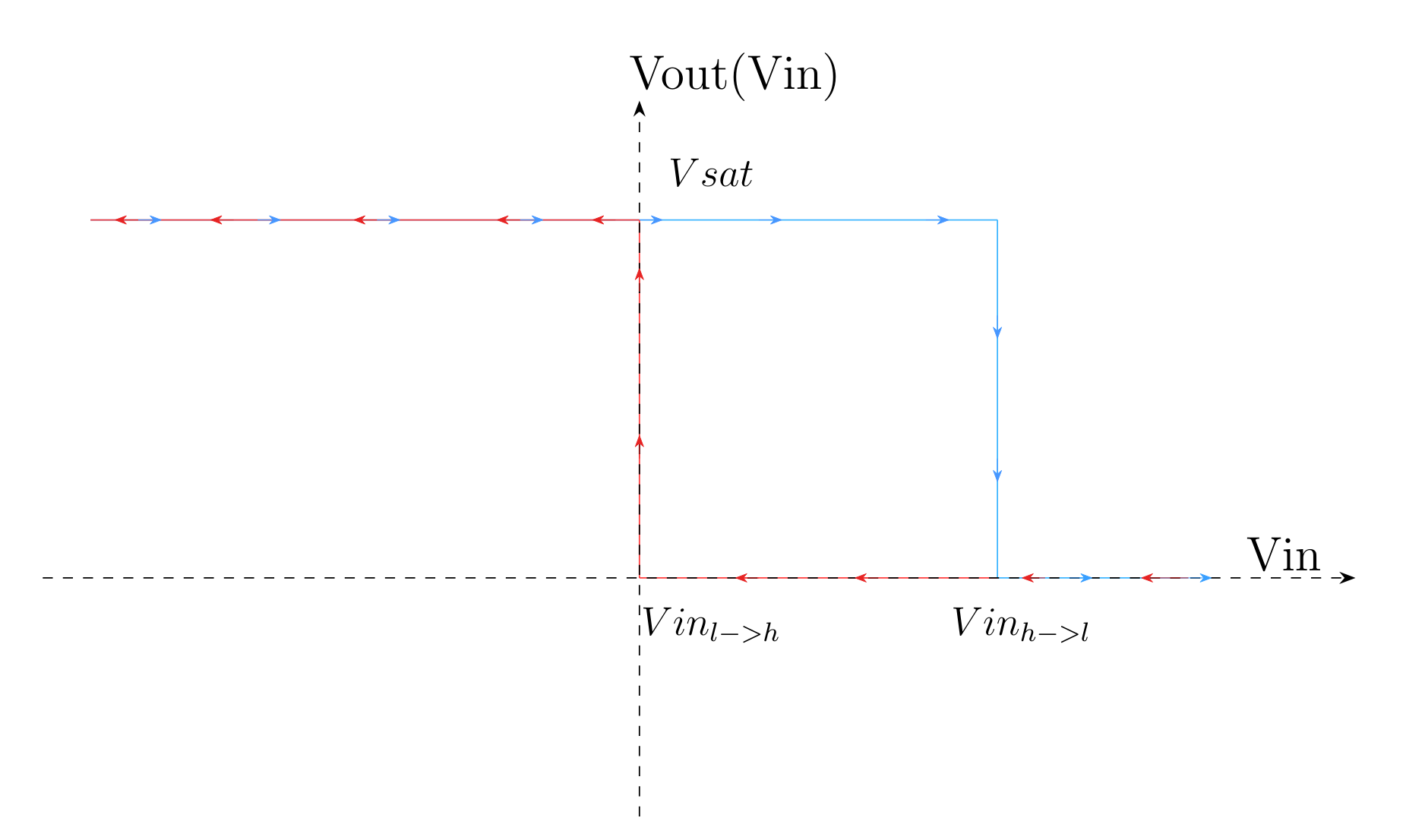
Schema
Hysteresis Comparator

\(Vin_{l->h} \text{ and } Vin_{h->l}\) represent the threshold voltages for switching from 0V to Vsat and from Vsat to 0V, respectively. Here, Vsat = 5V, which is the op-amp's supply voltage.

It is then shown that \(Vin_{h->l} = \frac{R_{6}}{R_{5} + R_{6}} Vsat\) and \(Vin_{l->h} = 0\). The proofs can be found in section 7.2 - Demonstrations.

Schema
Comparator Hysteresis Cycle
3.2.3 - Simulation of the Closed-Loop Circuit
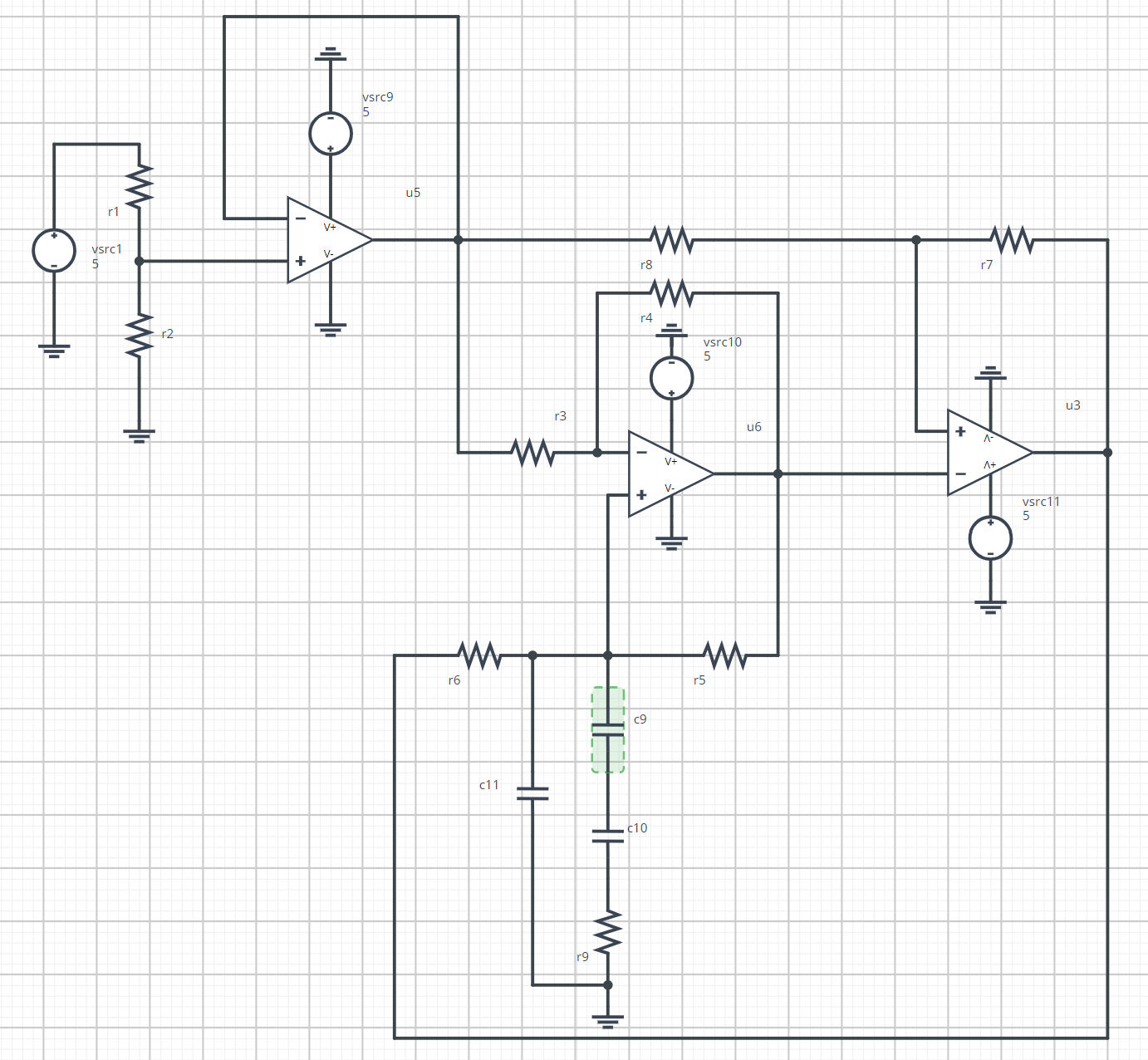
Schema
Conditioner Circuit Design in PartQuest

The simulation is carried out by varying the distance between the electrode and the hand from 1mm to 10 cm:

Schema
Simulation result with varying distance between electrode and hand (x-axis: distance, y-axis: frequency)

3.3 - PCB Design in KiCAD

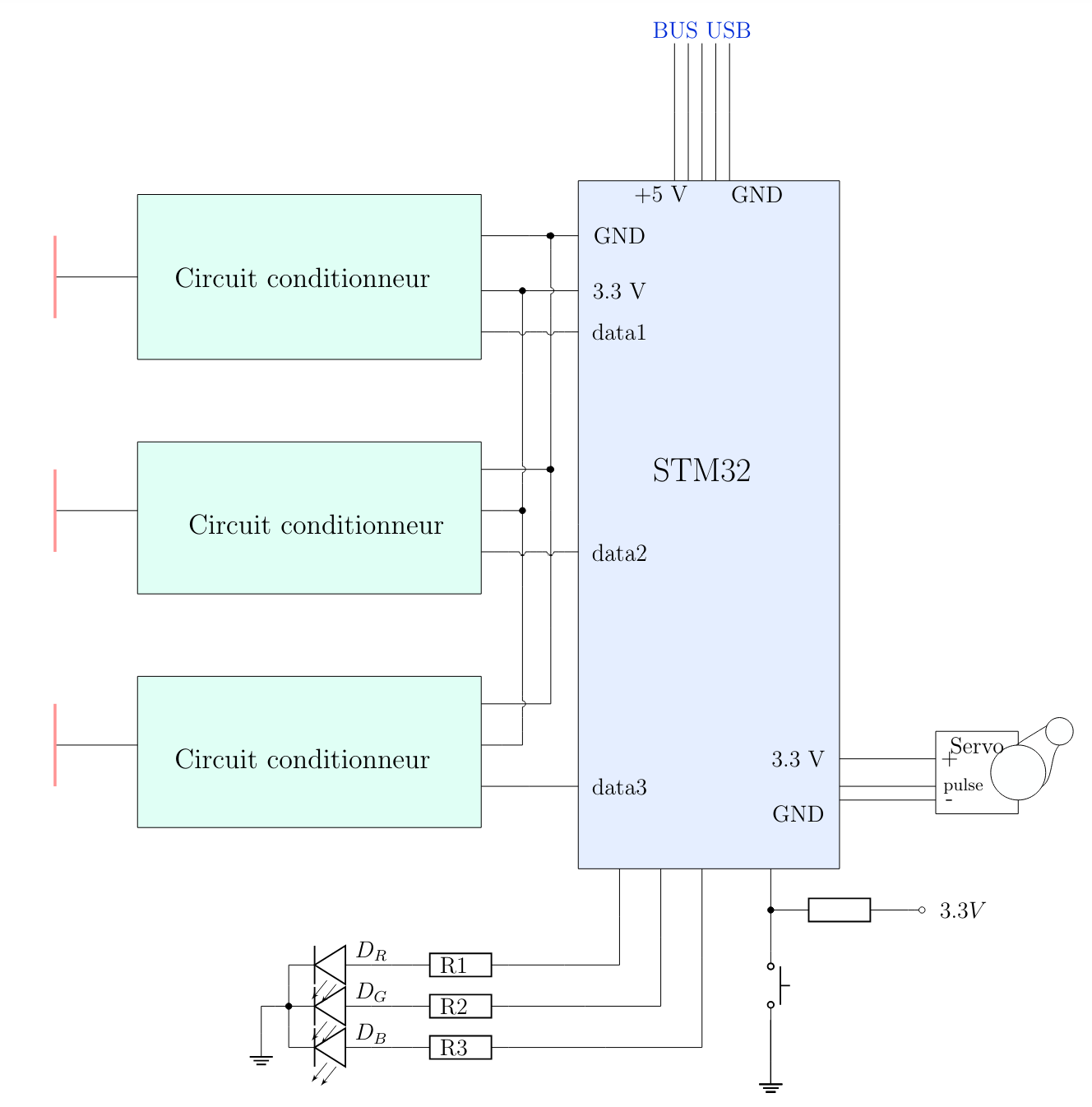
The PCB design was completed in two stages. First, we designed the full circuit for our project, consisting of a main STM32 connected to three conditioners at the input, along with an RGB LED, a button, and a test point output. Initially, we routed the entire project on a single PCB (including the three conditioners, the STM32, and all the outputs).

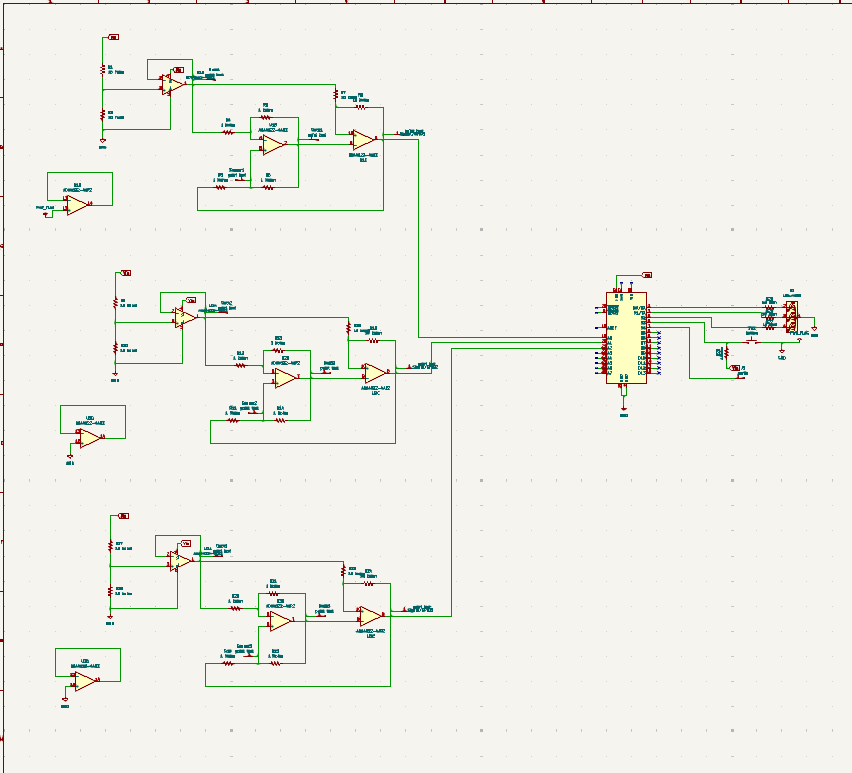
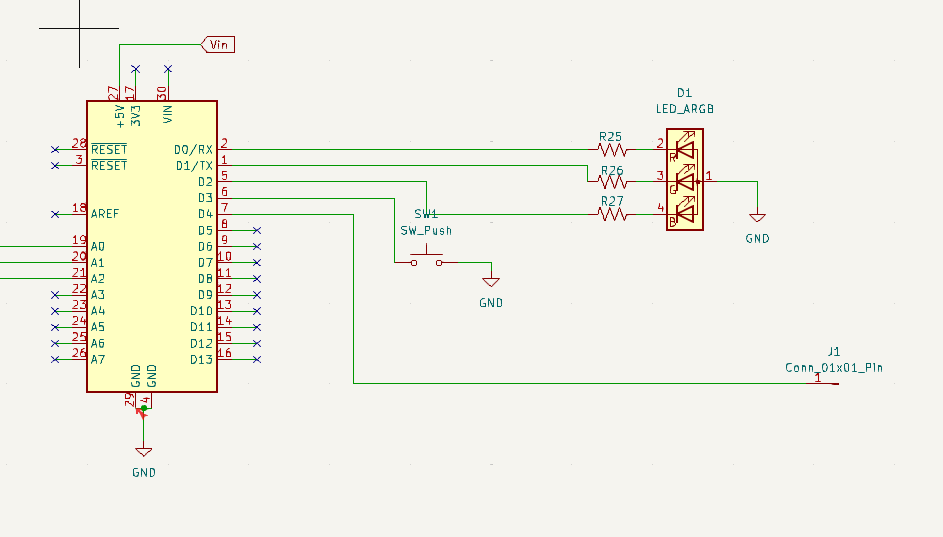
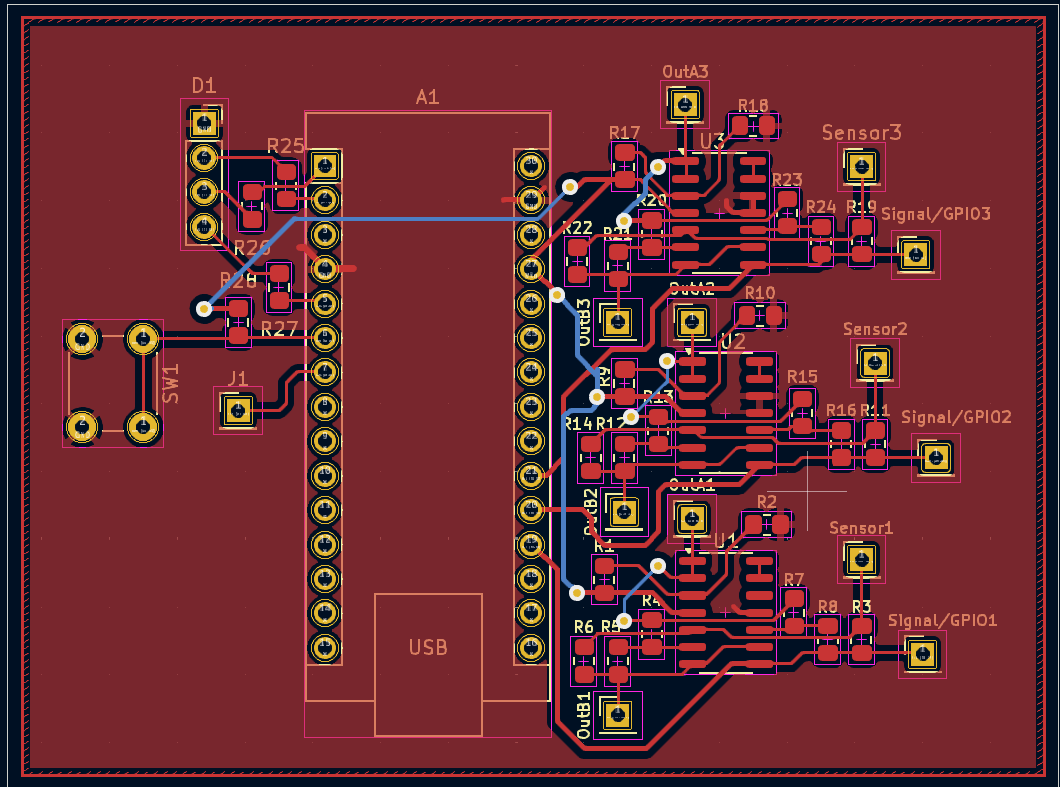
Schema
Project circuit with the 3 detailed conditioners
Schema
Zoom on STM32 outputs
Schema
Zoom on one of the conditioners
Schema
Circuit routing

However, due to a lack of op-amps, we were advised against printing our PCB and soldering the entire assembly. We were encouraged to redo the routing by integrating pre-made conditioners directly. This method allowed us to simplify the development process, avoid errors, and streamline the manufacturing process.

We decided to replace the conditioners with STM32 microcontroller footprints to use pre-made conditioners. As part of this optimization, we also replaced the RGB LED and button footprints, which gave us more freedom in the design of our project by removing constraints related to the accessibility of certain PCB sections. We then started the routing from scratch.

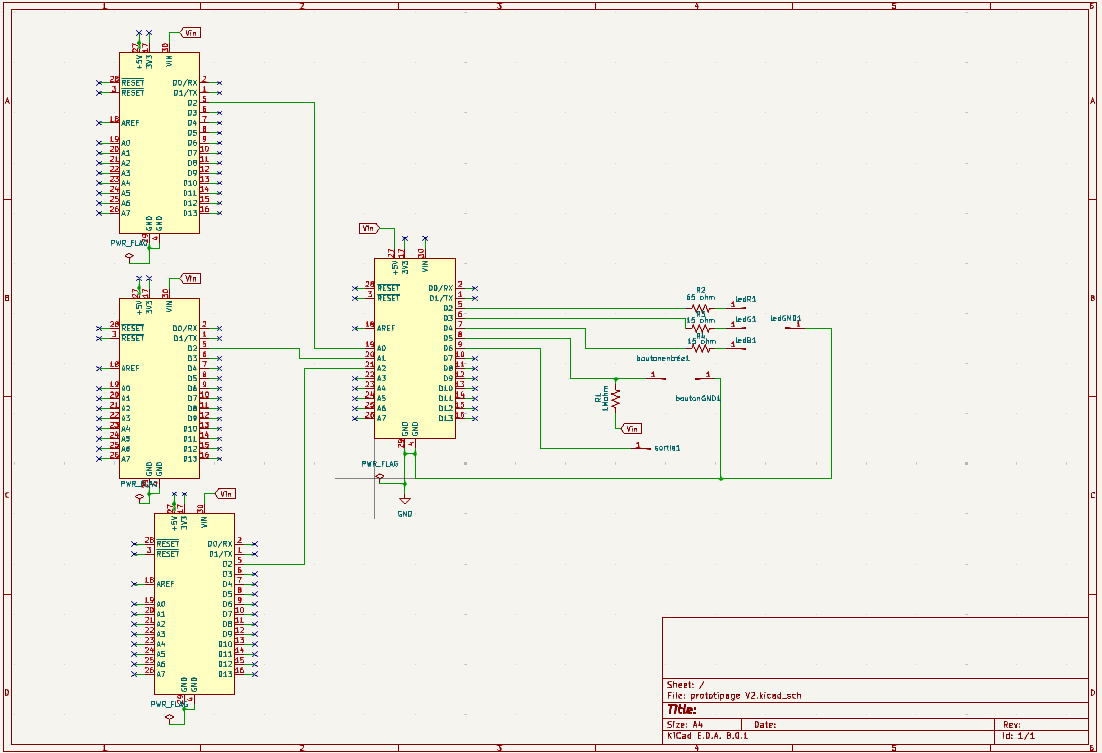
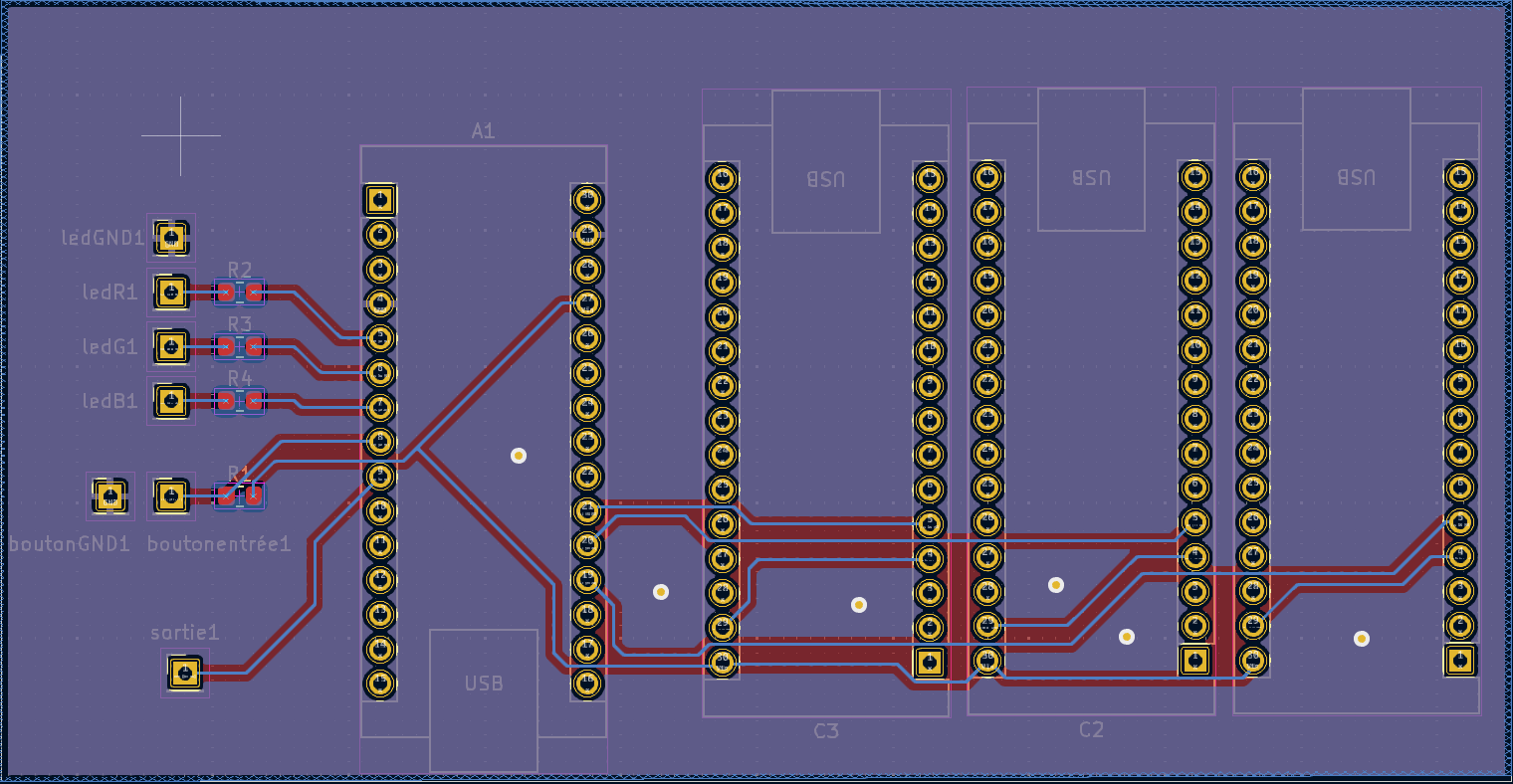
Schema
Circuit with STM32 microcontrollers instead of conditioners
Schema
Circuit routing

This method posed new problems, particularly with the orientation of the footprints to match the pre-made conditioners. After many corrections, we finally validated our PCB, which was sent for printing. This version would become the basis for our prototyping project. We also faced a shortage of conditioners and had to route two ourselves. This method caused significant delays and pushed back our testing phases, as the lack of PCB and conditioners limited the progress of our project.

3.4 - Tests and Measurements

After assembling our conditioner, we can test the frequency change at the circuit output.

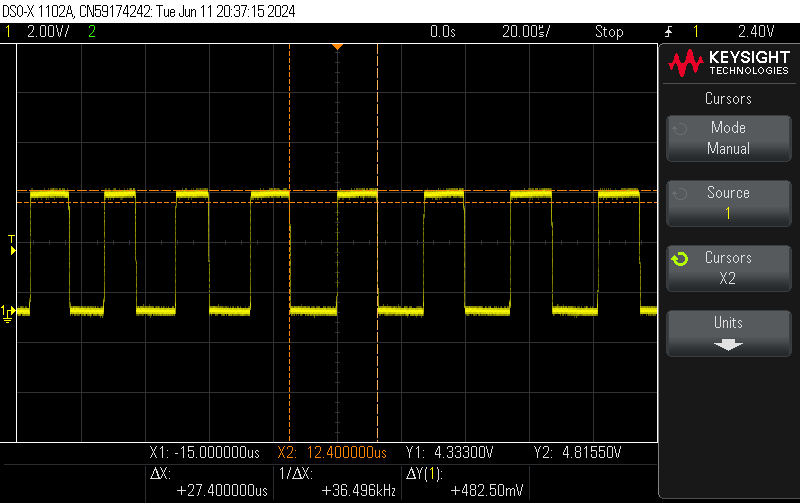
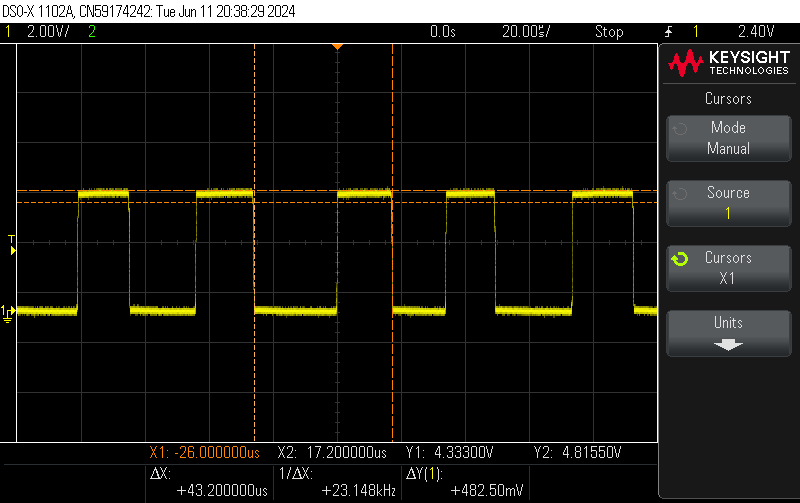
Schema
Conditioner output without any input
Schema
Conditioner output with a hand present

It is observed that without a hand nearby, the frequency is 36 kHz, whereas when the hand is brought closer to the copper plate, the frequency decreases to 23 kHz, for example.

The frequency has indeed decreased as expected when the hand approaches the copper plate.

4 - Signal Acquisition with an STM32 Microcontroller

4.1 - Overall Architecture of the Acquisition Code

To acquire the signal, we use the STM32 microcontroller. To determine the frequency, we use a timer that measures the time between two rising edges using an interrupt. This way, we can determine the frequency and then the capacitance using the relation \(f = \frac{1}{RC}\), with R = 1 M\(\Omega\).

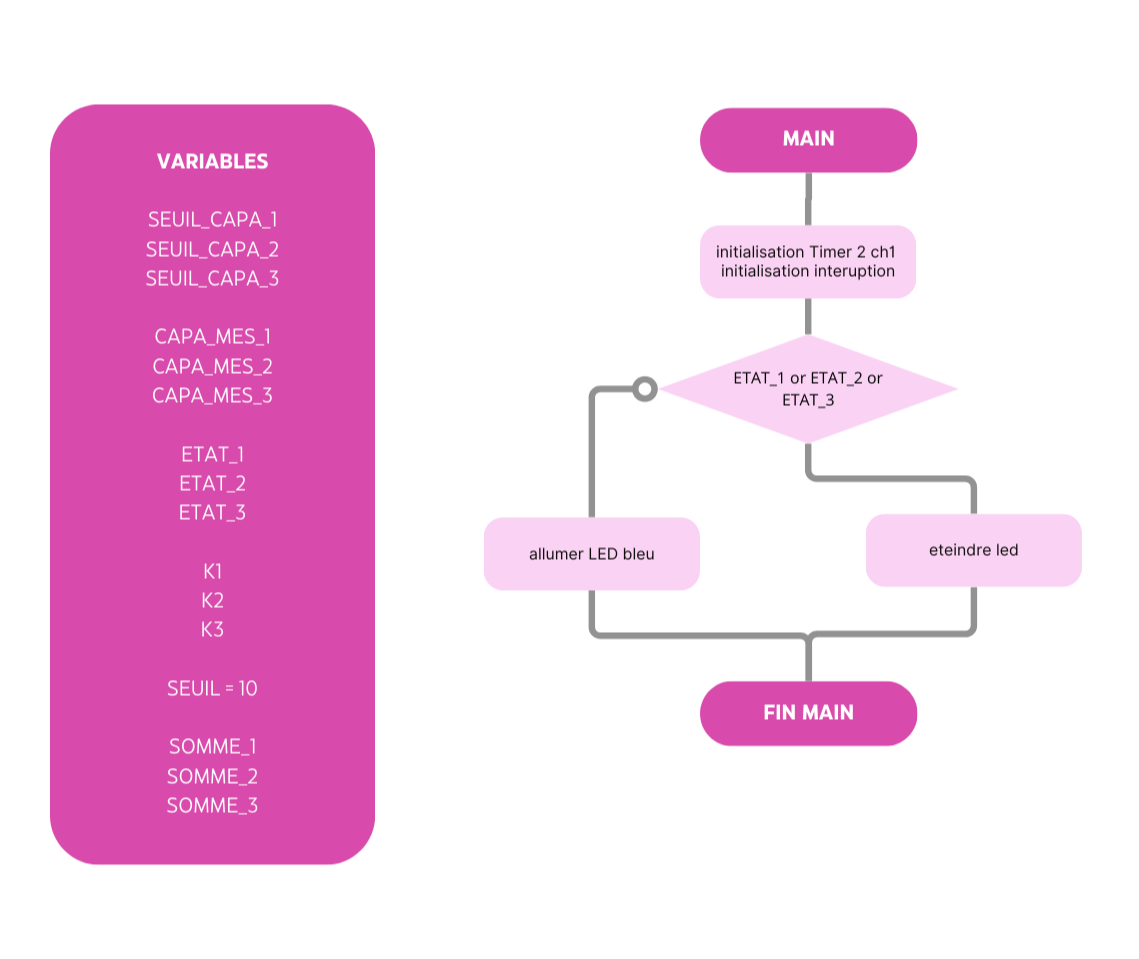
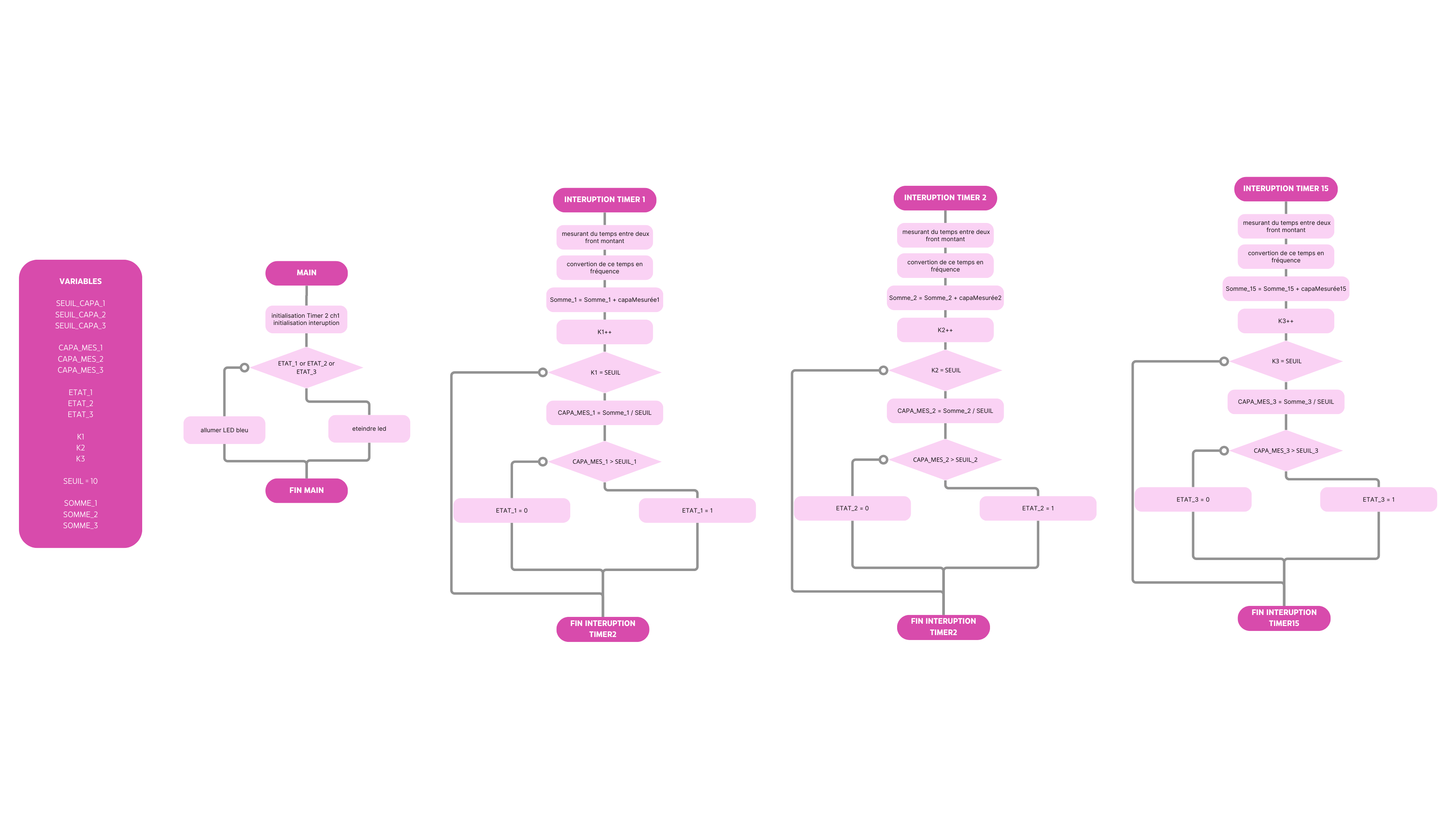
Schema
Main diagram
Schema
Interrupt diagram

For more precision, we can refer to the following diagram that details the frequency/capacitance acquisition using the timer:

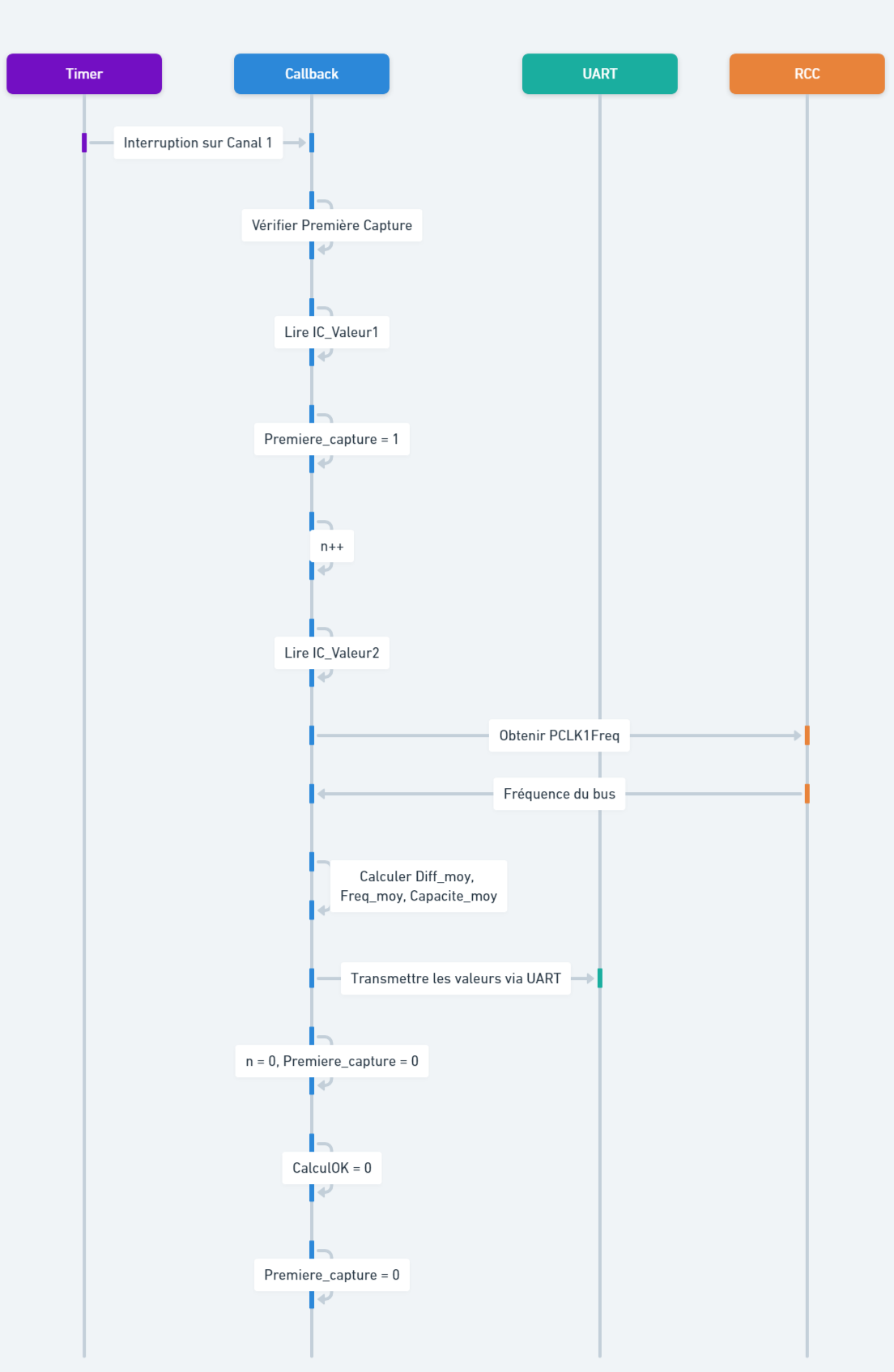
Schema
Interrupt diagram

For the design, we used UART transmission to visualize the capacitance values. However, we encountered several issues. The STM32 F301K8 board is a "MCU selector" and not a "Board selector," which prevented us from seeing certain connections, particularly that of UART1, which is used for the ST-LINK. We were blocked because UART1 was unusable. After some research, we found that we needed to use UART2 to transmit the data.

We do not use a prescaler, and we set the ARR to a very large value (8000000). We also enabled the 'NVIC' option for the interrupt and the Callback function.

5 - Finalization of the Project

5.1 - System Testing and Measurements

After programming the microcontroller, we took several measurements to characterize the proper functioning of our system.

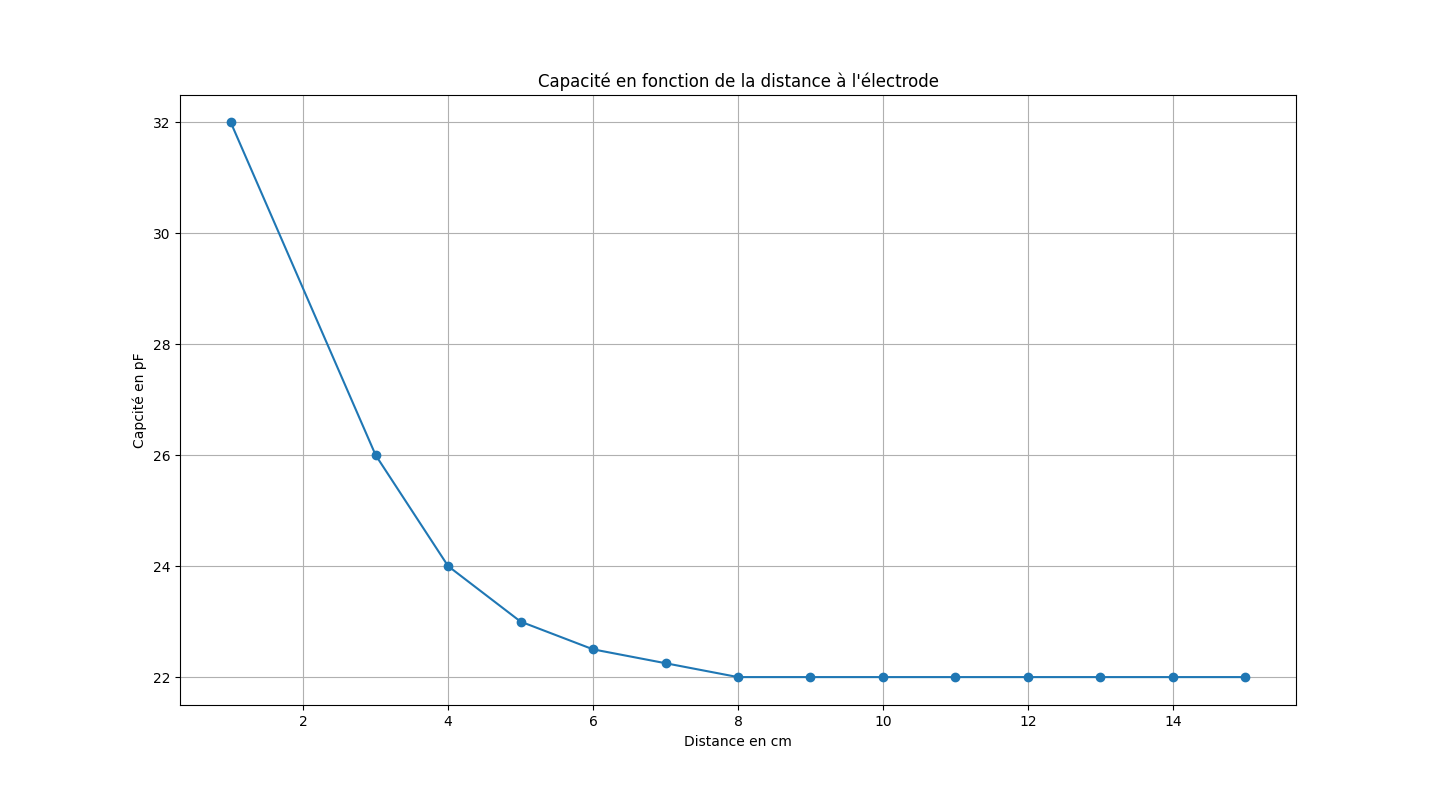
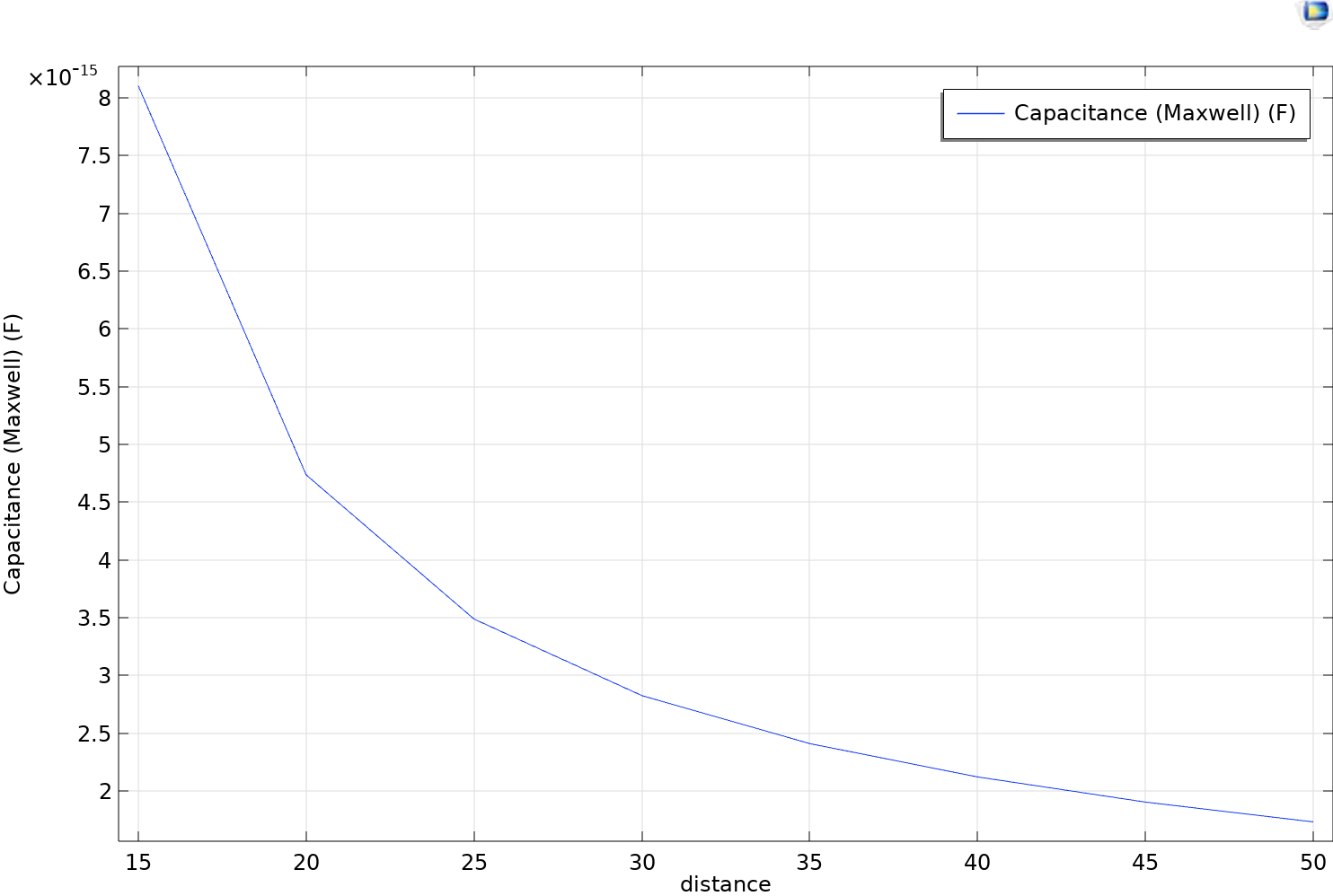
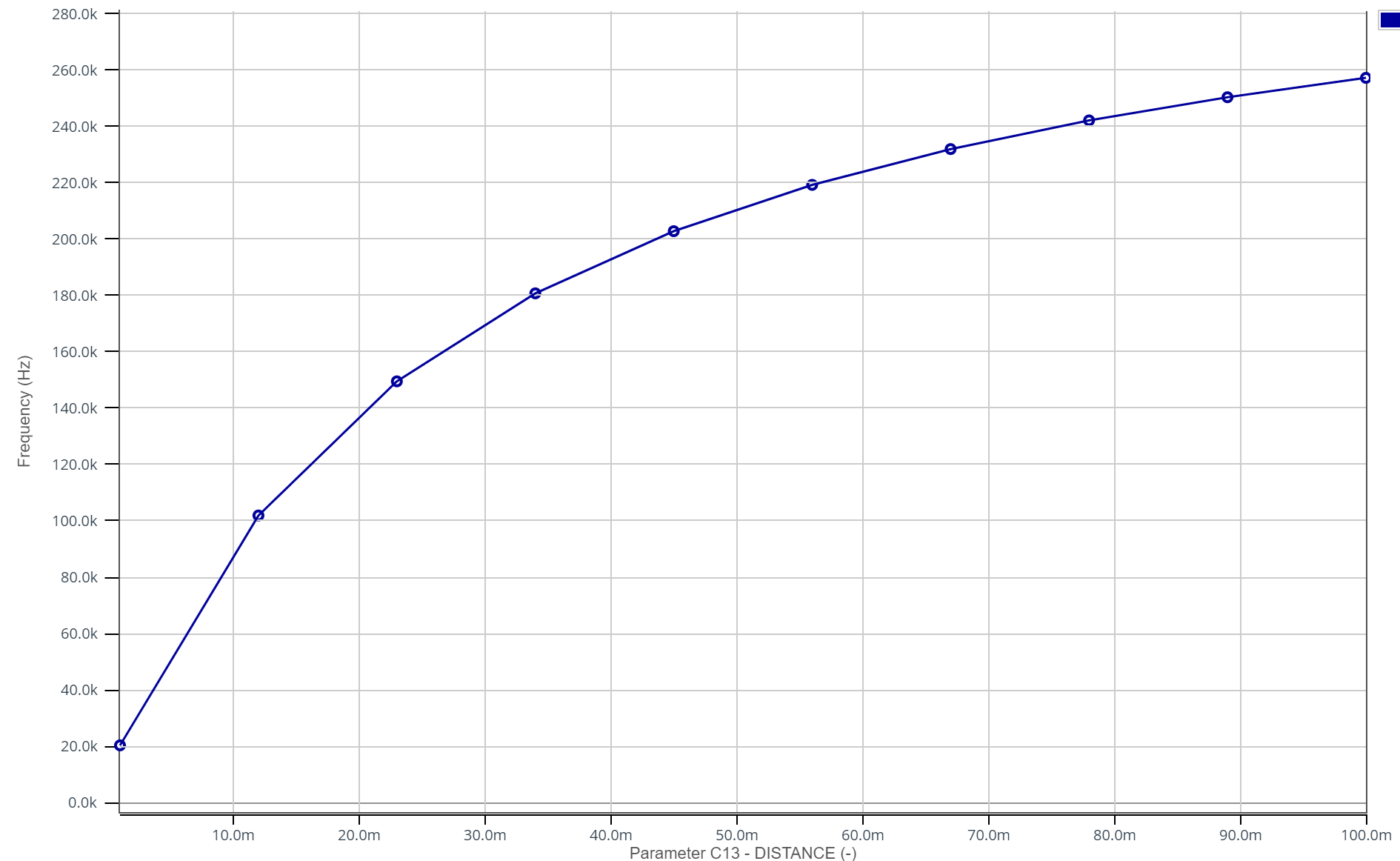
Schema
Capacitance as a function of distance plotted in Python

We measured the capacitance at regular intervals and then plotted it as a function of the distance. We observe that the shape and values are consistent with the theoretical ones.

It is noted that beyond 8 cm, the variation in capacitance is almost zero, making any further measurements inaccurate. Therefore, we will ensure not to exceed this value when setting the detection threshold for the two hand positions above the electrode. The closer the threshold is to 0 cm, the more precise the system will be, but it also becomes more difficult for the user to correctly position their hand in the two positions: it is then a matter of finding a compromise between precision and ergonomics.

We detect two positions for the hand: close or far:

Schema
LED lit blue for the close hand position
Schema
LED lit green for the far hand position

The color of the LED helps the user position their hand at the correct distance from the electrode to "enter" the desired code.

This system works for the three electrodes, allowing the user to input the desired code and perform the required action.

To ensure the correct hand position, the microcontroller performs several measurements before lighting up the LED in the correct color. This reduces the number of errors and improves the system's accuracy.

5.2 - Final Manufacturing

Schema
3D modeling of the project

We modeled a 3D-printed case that houses the microcontroller as well as the three conditioners for the three electrodes.

The RGB LED is located on the top and lights up to alert the user to the correct position of their hand or not.

Finally, our actuator is a servo motor that opens a small door, which in a real-world scenario could be a larger door to access a sensitive area, for example.

6 - Conclusion and Future Improvements

In conclusion, the objectives set at the beginning of our project were not fully achieved, but we made significant progress nonetheless. Unfortunately, the safety objective could not be fully addressed due to the technical difficulties encountered during the PCB fabrication and the development of the code. These obstacles prevented us from tackling this crucial topic.

However, our conditioner allowed us to avoid physical contact, ensuring good hygiene. Nevertheless, this aspect could still be improved. By optimizing the conditioner, we could increase the distance between the hand and the copper plate, thus offering better protection and comfort for the users.

Moreover, the ergonomic simplicity of our project fully met our goal of intuitiveness. This approach facilitated the use of our device, making interactions more natural and accessible for everyone. We are confident that these solid foundations will allow us to overcome the challenges faced and make future improvements to achieve all the initial objectives.

The prospects for this system include several potential improvements. First, optimizing the conditioner and signal management could further improve the system's accuracy and reliability.

Second, the integration of a more intuitive user interface could ease the use of the keypad.

Finally, expanding this system to other security and access applications could broaden its range of uses and make it more versatile in various contexts.

7 - Appendices

7.1 - Code Appendices

7.2 - Demonstration

Expression of the Capacitance of a Parallel Plate Capacitor

Symmetry of the electric field: For an infinite parallel plate capacitor, the plates are infinite and uniformly charged. This implies that the electric field \(\vec{E}\) must be perpendicular to the plates and uniform between them, due to the translational invariance in directions perpendicular to the plates. Gauss's law is given by: \[ \iint_{\Sigma} \vec{E} \cdot \vec{dS} = \frac{Q_{int}}{\epsilon} \] To apply this law, we consider a Gaussian surface in the shape of a cylinder passing through the two plates, where the ends of the cylinder are parallel to the plates of the capacitor. The symmetry of the problem tells us that the electric field is constant and perpendicular to the plates. For a plate with a surface charge density \(\sigma\), the total charge \(Q_{int}\) enclosed in the Gaussian surface is: \[ Q_{int} = \sigma \cdot S \] where \(S\) is the surface area of the ends of the cylinder. The contributions from the lateral sides of the cylinder cancel out, so the Gauss integral reduces to the two bases of the cylinder: \[ E \cdot S + (-E) \cdot (-S) = \frac{\sigma \cdot S}{\epsilon} \] \[ 2ES = \frac{\sigma S}{\epsilon} \] \[ E = \frac{\sigma}{2\epsilon} \] Calculation of the potential difference: The potential difference \(V\) between the two plates separated by a distance \(d\) is given by the integral of the electric field over this distance: \[ V = \int_{0}^{d} E \, dx = E \cdot d \] Using the charge density \(\sigma = \frac{Q}{S}\), where \(S\) is the surface area of a plate, we obtain: \[ V = \left(\frac{\sigma}{\epsilon}\right) \cdot d = \frac{Q}{\epsilon S} \cdot d \] Determination of the capacitance: The capacitance \(C\) of a capacitor is defined by the relation between the charge \(Q\) and the potential difference \(V\): \[ C = \frac{Q}{V} \] Substituting the expression for \(V\) that we found: \[ C = \frac{Q}{\frac{Qd}{\epsilon S}} = \frac{\epsilon S}{d} \] We have demonstrated that the capacitance of an infinite parallel plate capacitor, with a distance \(d\) between the plates and a surface area \(S\), is given by: \[ C = \frac{\epsilon S}{d} \]

Constant Current Generator

According to Millman's theorem: \[V_{-} = V_{out}\frac{R_{1}}{R_{1}+R_{1}}\] \[V_{+} = \frac{\frac{V_{in}}{R_{4}}+\frac{V_{out}}{R_{3}}}{\frac{1}{R_{4}}+\frac{1}{Z_{c}}+\frac{1}{R_{3}}}\] Moreover, since the op-amp operates in a linear regime, we have \(V_{+} = V_{-}\). Thus, \[ V_{+} = \frac{\frac{V_{in}}{R_{4}} + \frac{R_{1} + R_{1}}{R_{1} R_{3}} V_{+}}{\frac{1}{R_{4}} + \frac{1}{Z_{c}} + \frac{1}{R_{3}}} \] \[ \Rightarrow V_{+} = \frac{V_{in}}{R_{4}\left(\left(\frac{1}{R_{4}} + \frac{1}{Z_{c}} + \frac{1}{R_{3}}\right) - \frac{R_{1} + R_{1}}{R_{1} R_{3}}\right)} \Rightarrow V_{+} = \frac{V_{in}}{1 + \frac{R_{4}}{Z_{c}d} + \frac{R_{4}}{R_{3}} - \frac{R_{4}(R_{1}+R_{1})}{R_{1}R_{3}}} \] Now, by Ohm's law: \[ i = \frac{V_{+}}{Z_{c}} = \frac{V_{in}}{Z_{c} + R_{4} + \frac{Z_{c} R_{4}}{R_{3}} - \frac{Z_{c} R_{4}(R_{1} + R_{1})}{R_{1} R_{3}}} \] We want the current \(i\) to be independent of the capacitance impedance, so we must have: \[ Z_{c} + \frac{R_{4} Z_{c}}{R_{3}} - \frac{Z_{c} R_{4}(R_{1} + R_{1})}{R_{1} R_{3}} = 0 \] Hence, we get: \[ \boxed{i = \frac{V_{in}}{R_{4}}} \]

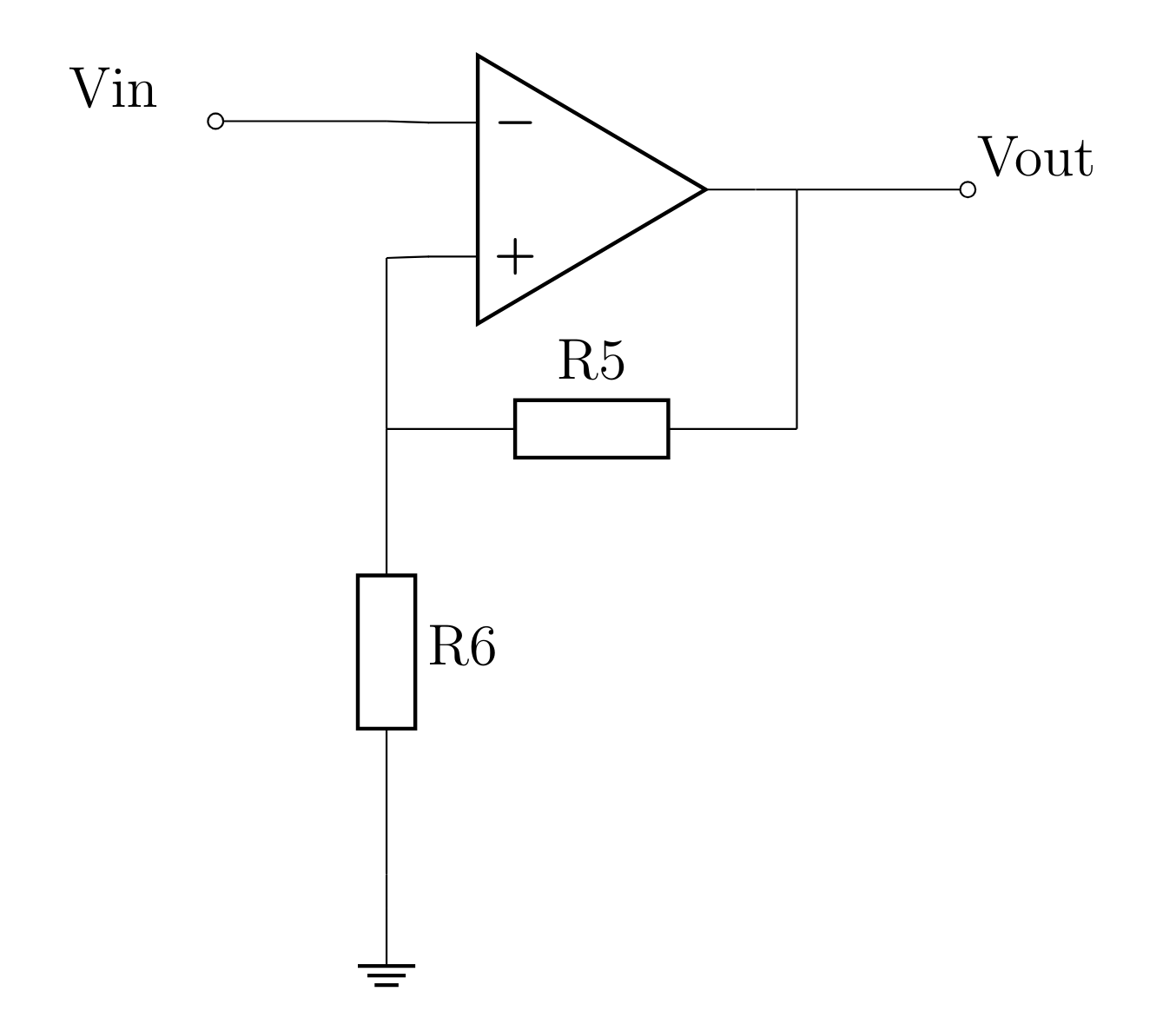
Hysteresis Cycle